12. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и CD, АС и BD, AD и BC, пересекаются в одной точке

§ 16. Параллельность прямых и плоскостей → номер 12

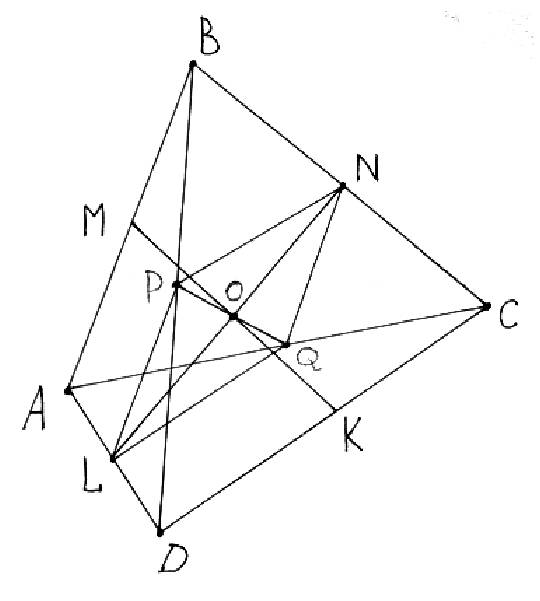
Пусть точки M, N, K, L, P, Q — середины отрезков AB, BC, CD, AD, BD, AC соответственно.

Из задачи №11 получаем, что отрезки МК и NL являются диагоналями параллелограмма MNKL с вершинами в серединах сторон четырехугольника ABCD. Значит, МК и NL пересекаются в некоторой точке O и делятся этой точкой пополам. Также отрезки PQ и NL являются диагоналями параллелограмма PNQL с вершинами в серединах сторон четырехугольника ABCD, образованного этими сторонами. Значит, PQ и NL пересекаются и в точке пересечения делятся пополам, а так как O — середина NL, то, значит, O — середина PQ. И PQ и NL пересекаются в точке O. Так что искомые прямые MK, NL и PQ, соединяющие середины отрезков AB и CD, BC и AD, AC и BD соответственно пересекаются в одной точке O, что и требовалось доказать.