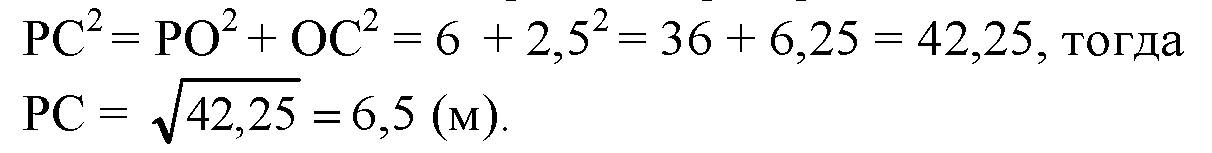§17. Перпендикулярность прямых и плоскостей → номер 20
Пусть АН высота равнобедренного треугольника АВС с основанием ВС и равными сторонами АВ = АС. Нарисуем ΔАВС на плоскости (1) и на проекционном чертеже (2). Пусть P данная точка.
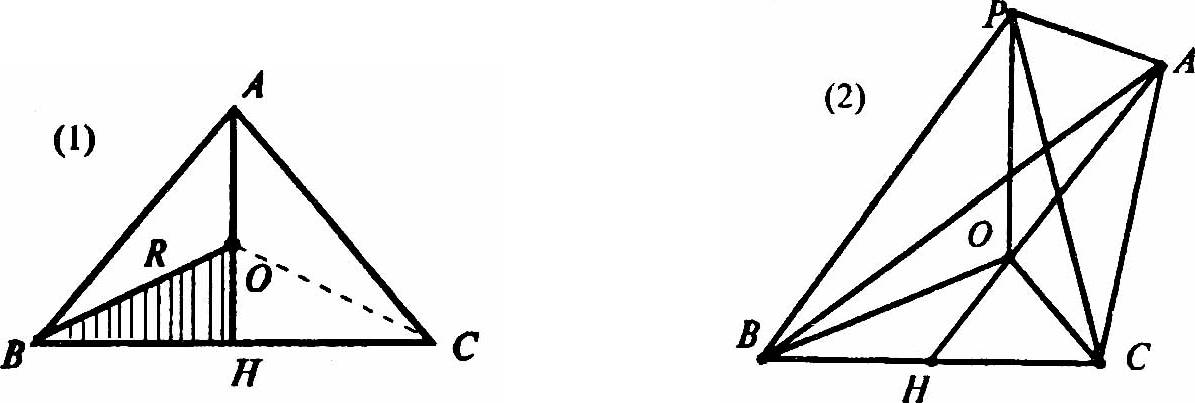
Так как точка Р равноудалена от точек А, В, С, т. е. РА = РВ = РС, то проекция О точки Р на плоскость αВС — центр описанной около ΔАВС окружности. Значит, точка О лежит на серединном перпендикуляре к стороне ВС, т. е. на прямой АН.
Рассмотрим ΔОВН. По теореме Пифагора:
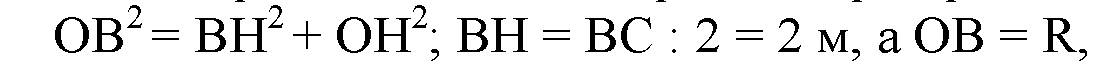
Тогда
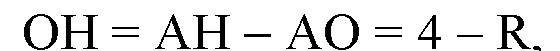
Получаем:
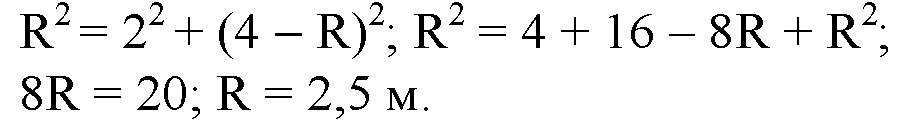
Далее в ΔPOC по теореме Пифагора: