34. 1) Докажите, что прямая, пересекающая параллельные плоскости, пересекает их под равными углами. 2) Докажите, что плоскость, пересекающая параллельные прямые, пересекает их под равными углами

§18. Декартовы координаты и векторы в пространстве → номер 34

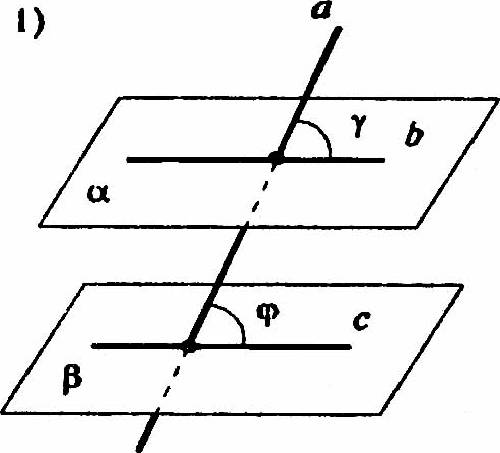
1) В параллельных плоскостях α и β, через точки пересечения их с данной прямой а проведем прямые b и с, параллельные между собой. Углы γ и φ равны (соответственные углы при параллельных прямых b и с, секущей а). Что и требовалось доказать.

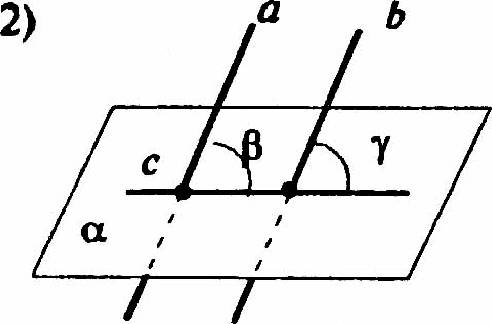
2) В плоскости α проведем прямую с, через точки пересечения ее с прямыми а и b.

Тогда угол β равен углу γ (соответственные углы при параллельных прямых а и b, секущей с). Что и требовалось доказать.