§18. Декартовы координаты и векторы в пространстве → номер 42
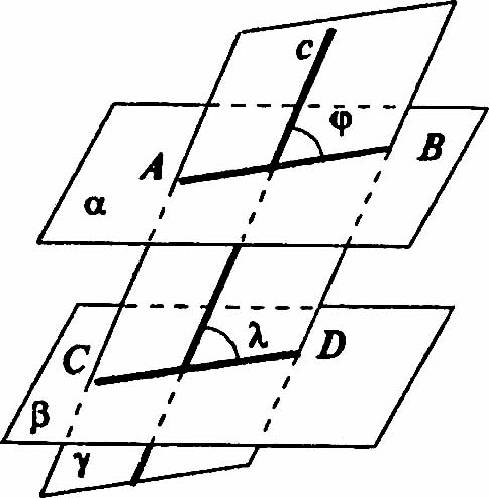
Пусть даны плоскости α || β и γ пересекает их по прямым АВ и CD соответственно.
Тогда АВ || CD (по свойствам параллельных плоскостей).
Из рисунка заметим, что углы φ и λ — искомы. Это линейные углы двугранных углов, образованных плоскостями α, β и γ
∠φ = ∠λ, так как это соответственные углы при параллельных прямых АВ и CD, и секущей с. Что и требовалось доказать.
