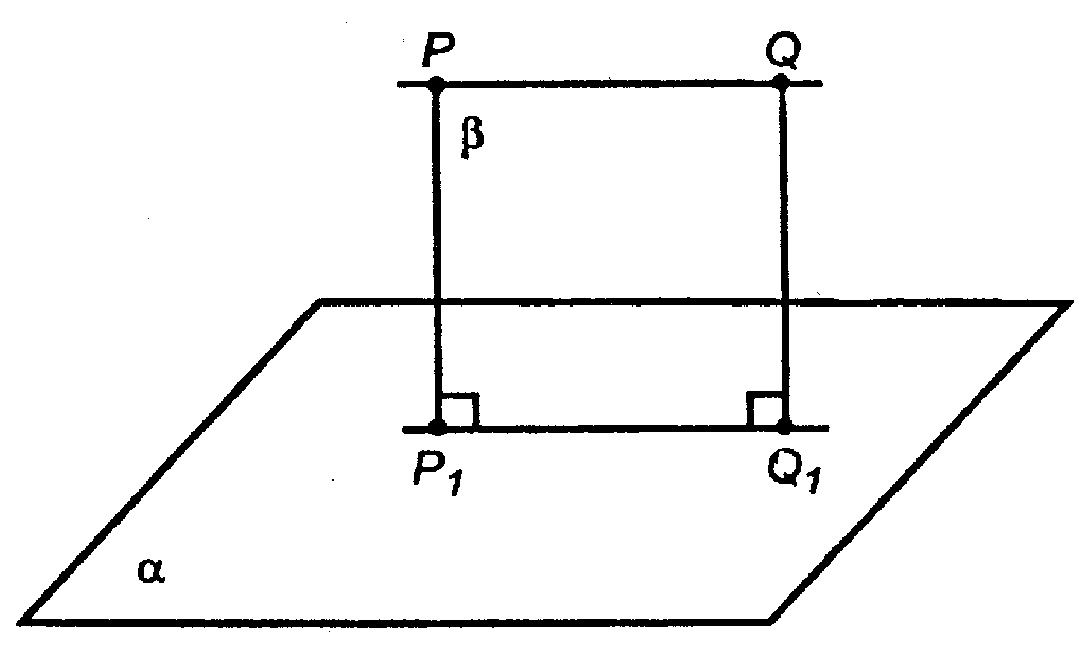
Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 124 124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках P1и Q1. Докажите, что PQ = P1Q1.
Дано:
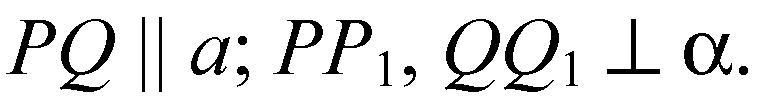
Решение:
PP1 || Q1Q, как перпендикулярные одной плоскости.
Следовательно, РР1 и QQ1 принадлежат одной плоскости. Назовем ее β. Пусть P1Q1 — линия пересечения плоскостей α и β.
Тогда
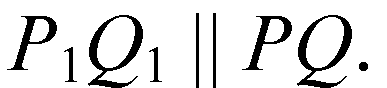
Таким образом, PQQ1P1 — параллелограмм, следовательно, PQ =
=P1Q1.
Что и требовалось доказать.
