Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 146
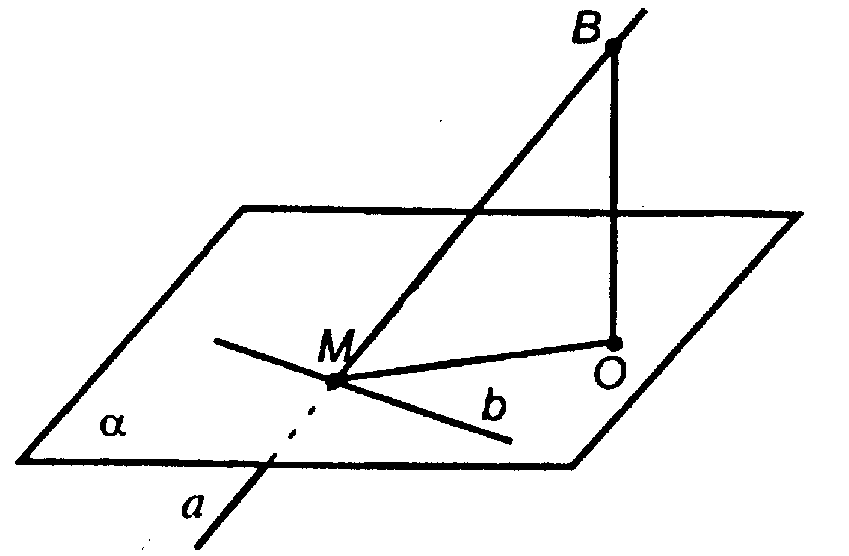
Дано: а ∩ α = М; а не перпендикулярна α.
Решение:
Если бы через т. М проходили две прямые, перпендикулярные к а, тогда по признаку перпендикулярности прямой к плоскости должно быть а ⊥ α, а по условию а не перпендикулярна α. Т. о. b — единственная прямая, которая, проходя через т. М, перпендикулярна а.
Что и требовалось доказать.
