Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 162 162. Прямая MA проходит через точку А плоскости α и образует с этой плоскостью угол φ0≠90°. Докажите, что φ0 является наименьшим из всех углов, которые прямая МА образует с прямыми, проведенными в плоскости α через точку А.
Решение. Обозначим буквой Н основание перпендикуляра, проведенного из точки М к плоскости α, и рассмотрим произвольную прямую р в плоскости α, проходящую через точку А и отличную от прямой АН (рис. 57). Угол между прямыми AM и р обозначим через φ и докажем, что φ>φ0
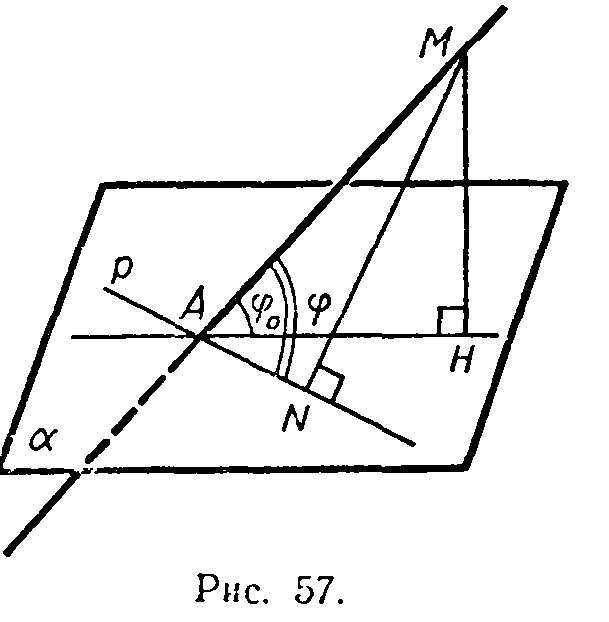
Из точки М проведем перпендикуляр MN к прямой р. Если точка N совпадает с точкой А, то φ = 90° и поэтому φ>φ0. Рассмотрим случай, когда точки А и N не совпадают (см. рис. 57). Отрезок AM — общая гипотенуза прямоугольных треугольников ANM и АНМ, поэтому sinφ=MN/AM, sinφ0=MH/AM. Так как MN>MH (MN — наклонная, МН —перпендикуляр), то из двух этих равенств следует, что sinφ>sinφ0 и поэтому φ>φ0.
