Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 176
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано:
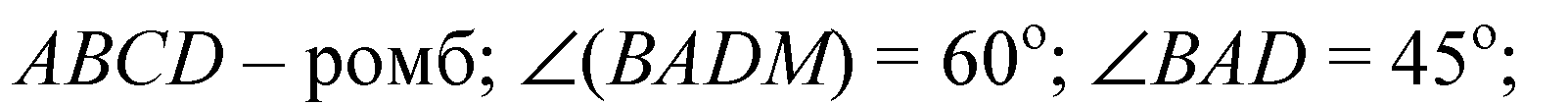
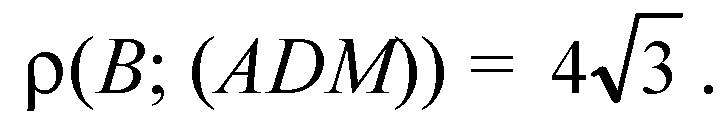
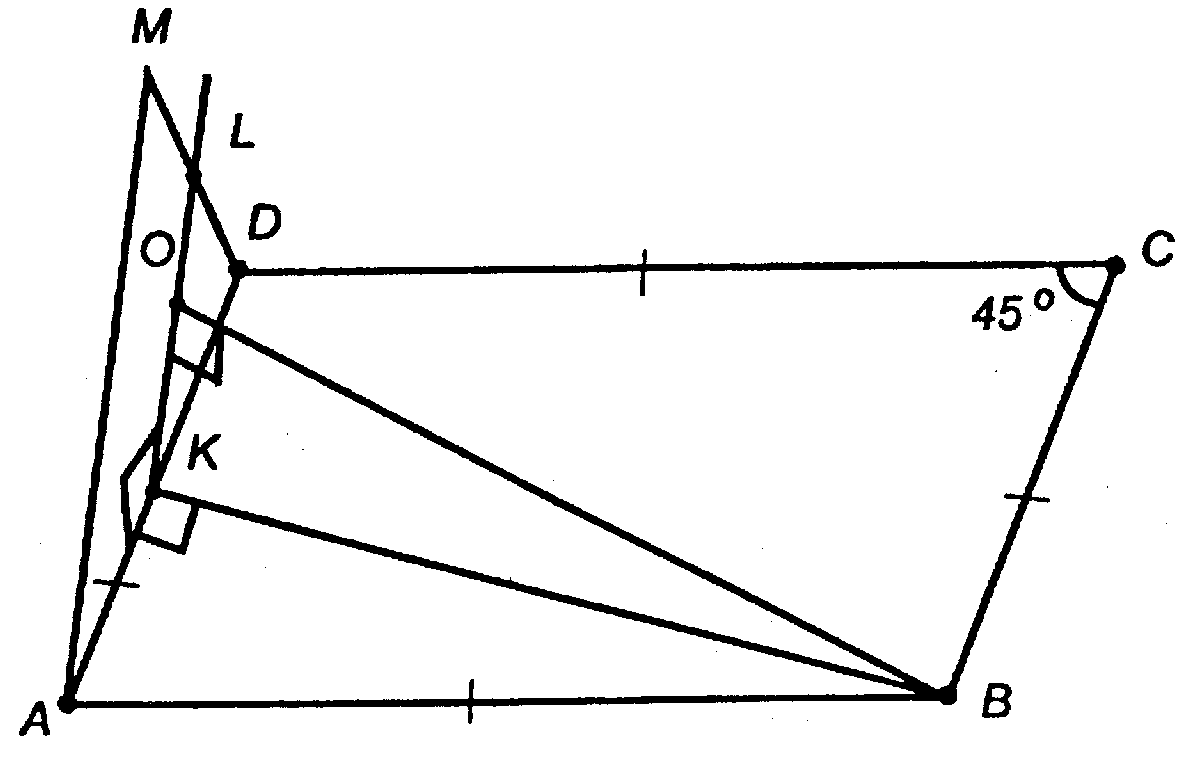
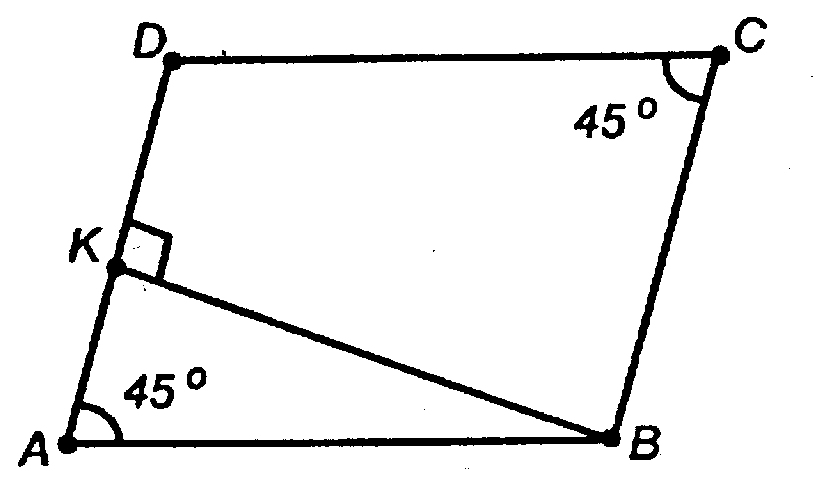
Решение:
Построим BK ⊥ AD.
В пл. ADM проведем KL ⊥ AD.
∠BKL — линейный угол двугранного угла BADM. ∠BKL = 60о (по условию).
В пл. BKL опустим на KL перпендикуляр ВО.
Докажем, что ВО ⊥ пл. ADM.
А)
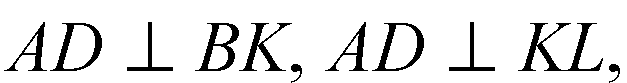
То
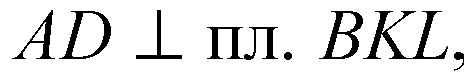
Следовательно, AD пер
Пендикулярна всем прямым в плоскости BKL, то есть
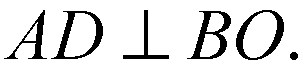
Б)
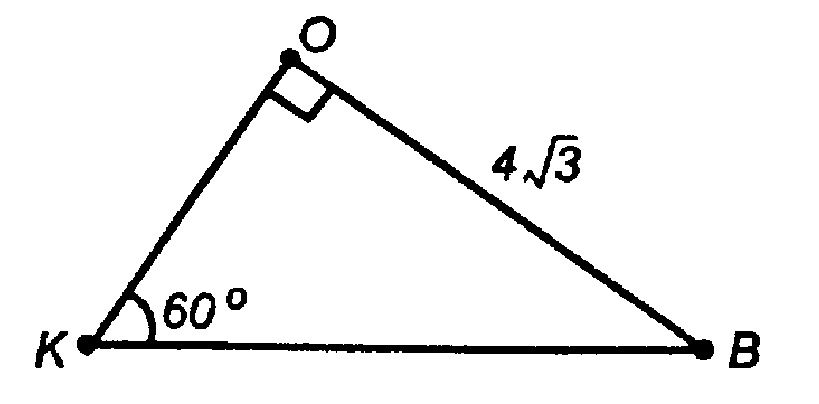
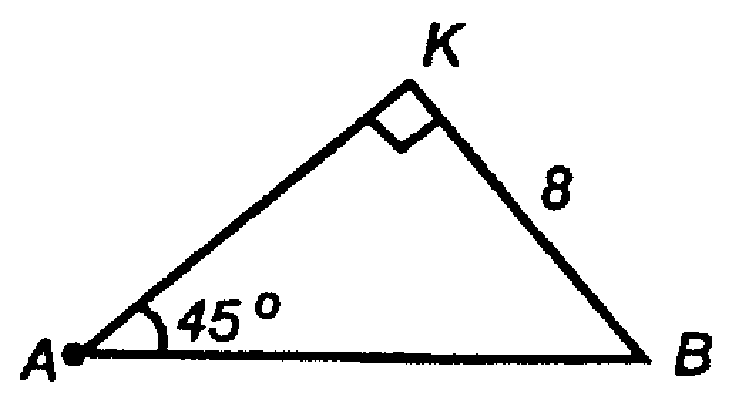
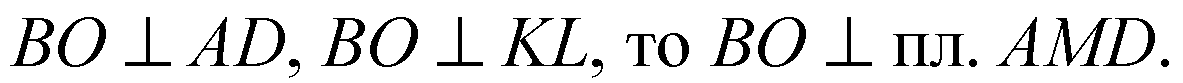
Итак,
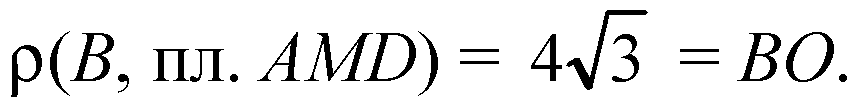
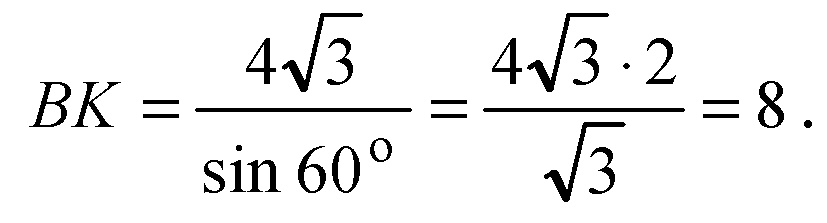
В пл. ABCD
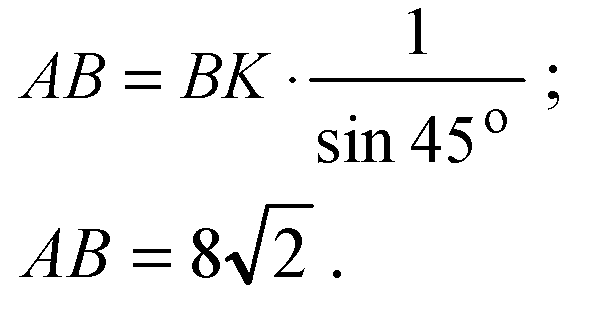
Ответ: