Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей. → номер 199
Дано:
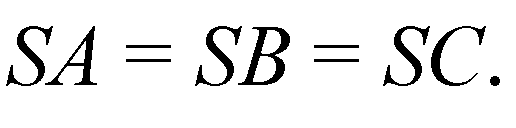
Решение:
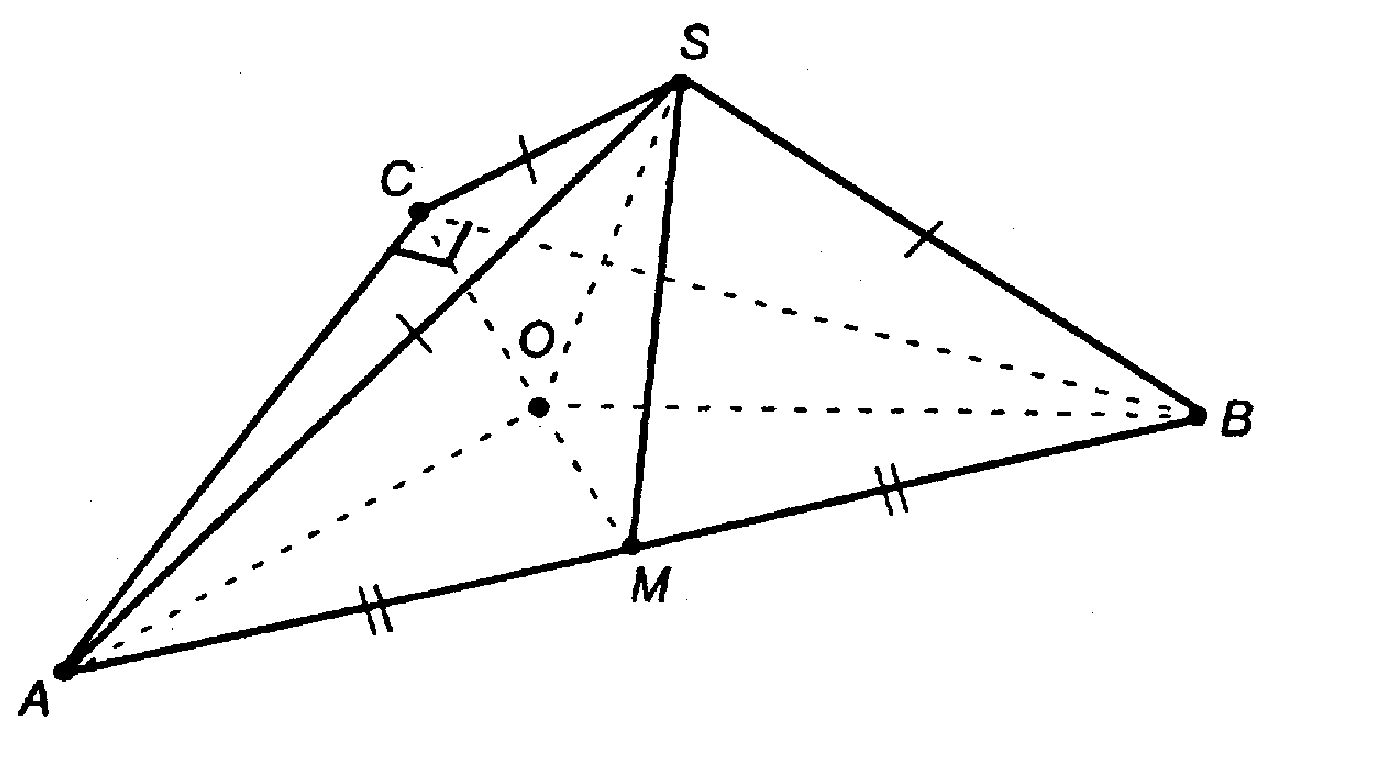
1. ΔASB — равнобедренный, SM — медиана, поэтому SM ⊥ AB (это высота).
2. Проведем отрезок СМ. в пл. SCM проведем SO L СМ. Точку О соединим с вершинами А, В и С.
AS, BS, CS — равный наклонные, поэтому их проекции также равны, то есть ОА = ОВ= ОС = R, R — радиус описанной окружности около ΔАВС.
Итак, SM ⊥ пл. АВС.
Что и требовалось доказать.
