Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей. → номер 210
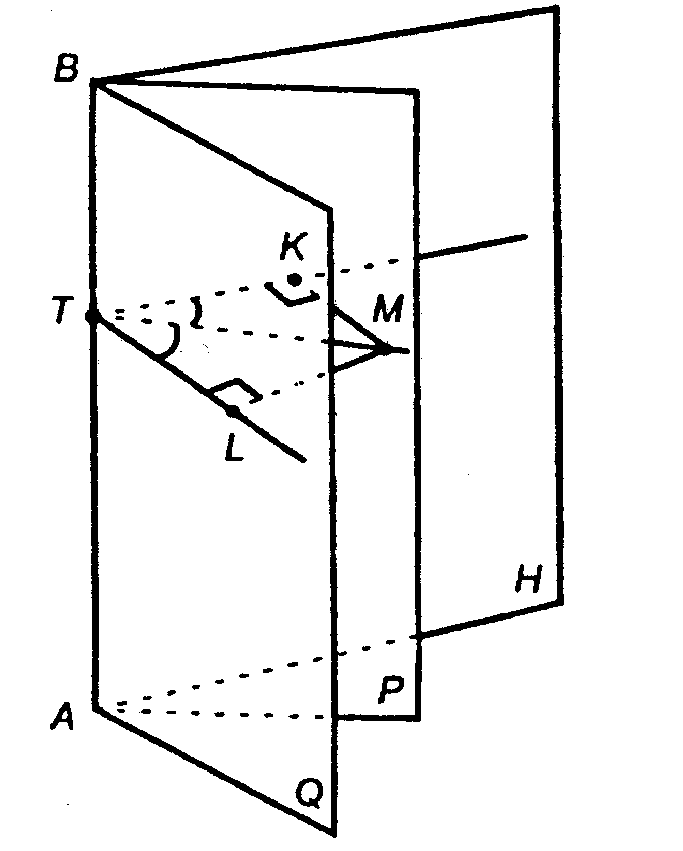
Решение:
1. Выберем произвольную т. М ∈ Р.
2. Проводим МТ ⊥ АВ.
В пл. АВН проводим KT ⊥ АВ.
В пл. ABQ проводим TL ⊥ AB.
3. ∠KTL — линейный угол двугранного угла HABQ; ∠KTM — линейный угол двугранного угла НАВР;
∠MTL — линейный угол двугранного угла PABQ;
∠KTM = ∠MTL — как линейные меры равных двугранных углов.
4. В пл. KTL проводим MK ⊥ TK, ML ⊥ TL.
5. ΔKTM и ΔLTM — прямоугольные, ТМ — общая, углы KTMи MTL равны. ΔKTM = ΔLTM, отсюда MK = ML.
Поскольку т. М выбрана произвольно, то доказанное справедливо для всех точек из пл. МВР.
Что и требовалось доказать.
