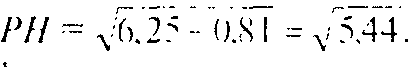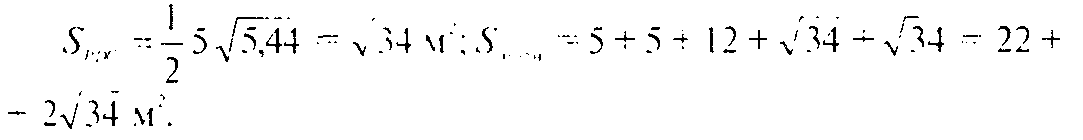241. Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды

Глава III Многогранники. § 2. Пирамида → номер 241

Пусть АВ = 5 м, АD = 4 м, BD = Зм и PO = 2 м. Заметим, что АВ2 = AD2 + BD2 и значит ∠BDA = 90°. Но OD — проекция PD на плоскость ABCD. Поэтому PD⊥AD(рис. 157).

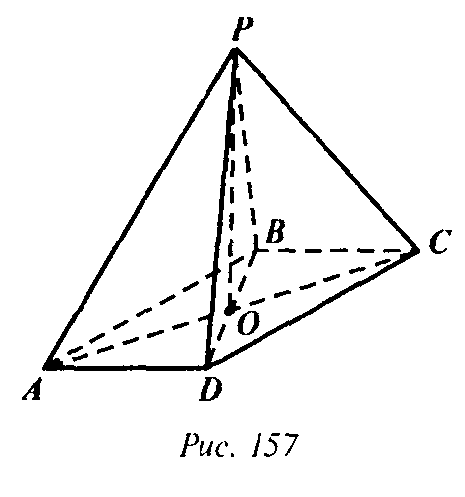
Аналогично PB⊥ВС. Найдем PD:

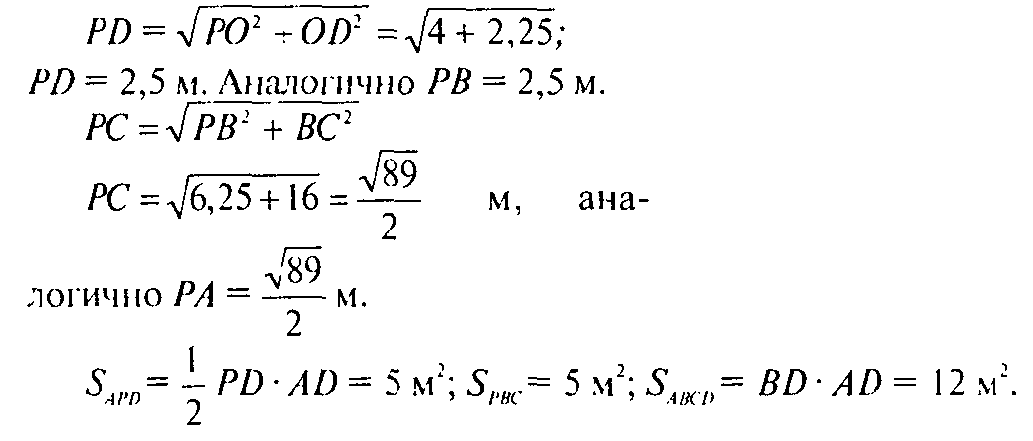
Найдем SPAB и SPDC: так как ΔPAB=ΔPDC ( по трем сторонам), то достаточно найти площадь одного из треугольников. Рассмотрим ΔPDC: проведем высоту PH (рис. 158).

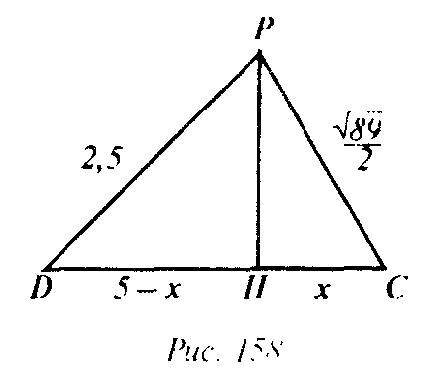
Пусть

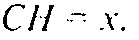
Тогда

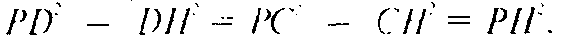
Таким образом

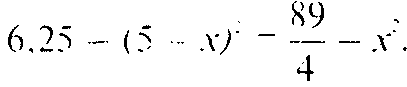
Отсюда

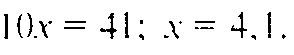
Тогда