Глава III Многогранники. § 2. Пирамида → номер 266
Проведем сечение через диагональ AC параллельно MD. Тогда прямая, по которой пересекаются плоскости сечения и BMD, параллельна MD. Поэтому это средняя линия НК треугольника BMD. Таким образом AKC искомое сечение, где К — середина ВМ (рис. 174а). Найдем стороны КС и АК: рассмотрим ΔМВС (рис. 174б):
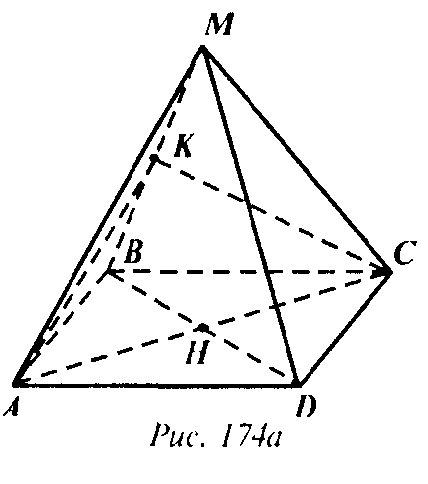
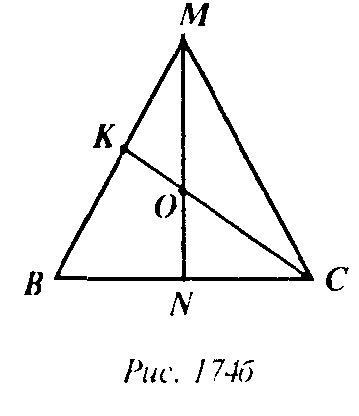
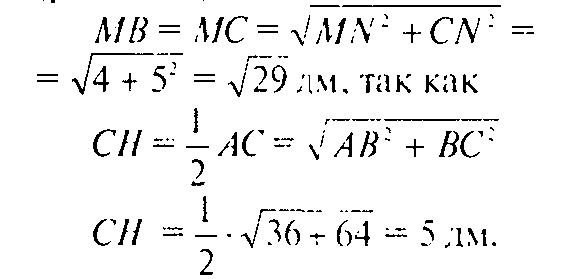
Проведем в ΔMBC высоту MN (она же является медианой).
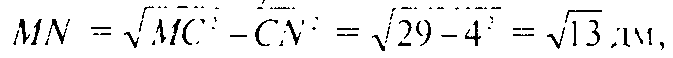
Так как
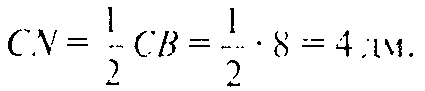
Так как точка О — точка пересечения медиан СК и MN треугольника MBC, то
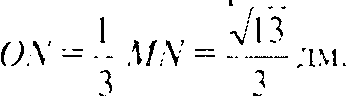
Тогда
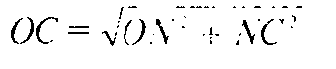
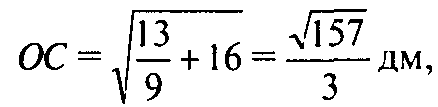
А так как
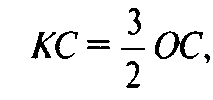
То
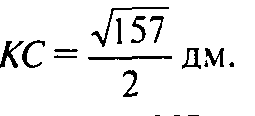
Аналогично из ΔAMB находится. что
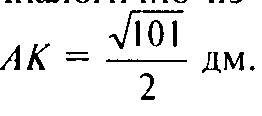
Таким образом в ΔAKC(рис. 174в)
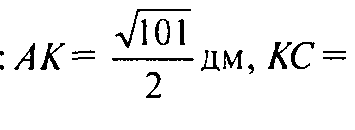
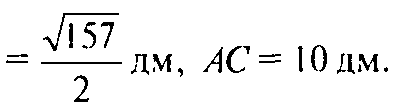
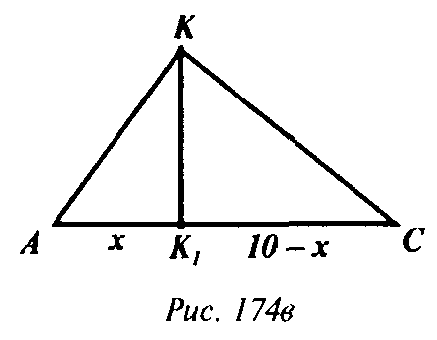
Проведем высоту
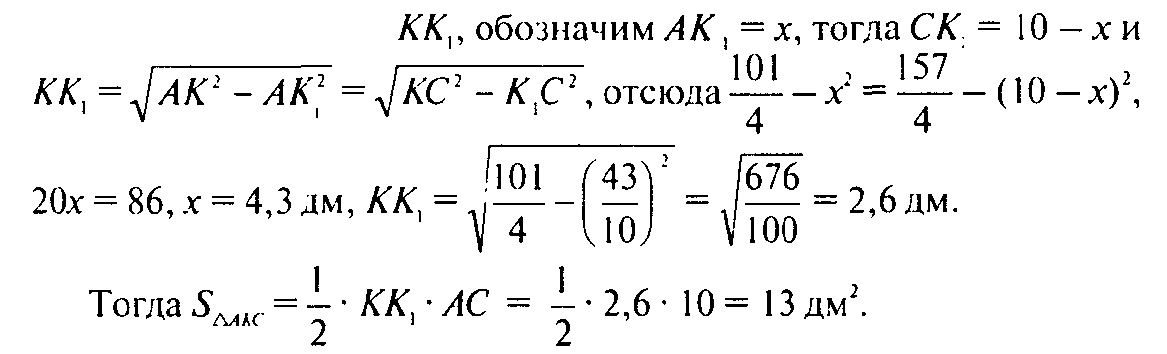
Ответ 13 дм2.
