Глава IV. Векторы в пространстве § 3. Компланарные вектора → номер 355 355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарны: а) АА1, СС1, ВВ1; б) АВ, AD, АA1; в) В1В, AC, DD1; г) AD, СС1, A1B1?
а) Отложим эти вектора от точки А. Тогда получится AA1, AA2, AA3 , но эти вектора, очевидно, лежат в одной плоскости. Поэтому AA1, CC1, BB1 компланарные вектора (рис. 213).
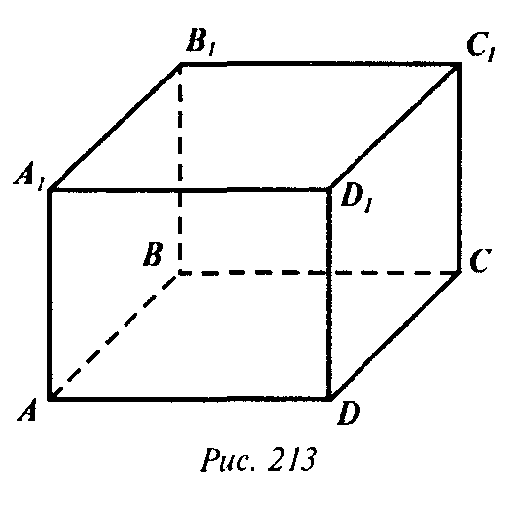
Б) Эти векторы уже отложены от одной точки А. Векторы АВ и AD лежат в плоскости ABCD, а вектор AA1 не лежит в этой плоскости. Поэтому AA1, AB, AD не компланарны. в) Отложим эти векторы от точки А. Тогда получатся векторы A1A2, AC, AA2, где А2 — симметричная точка к А1 относительно точки А. Очевидно, что данные три вектора лежат в плоскости АА1С1С. Поэтому и исходные вектора компланарны. г) Отложив эти вектора от точки А получим вектора AD, AA1, AB, которые не компланарны (см. п. б). Поэтому и вектора AD, CC1, A1B1 не компланарны.
