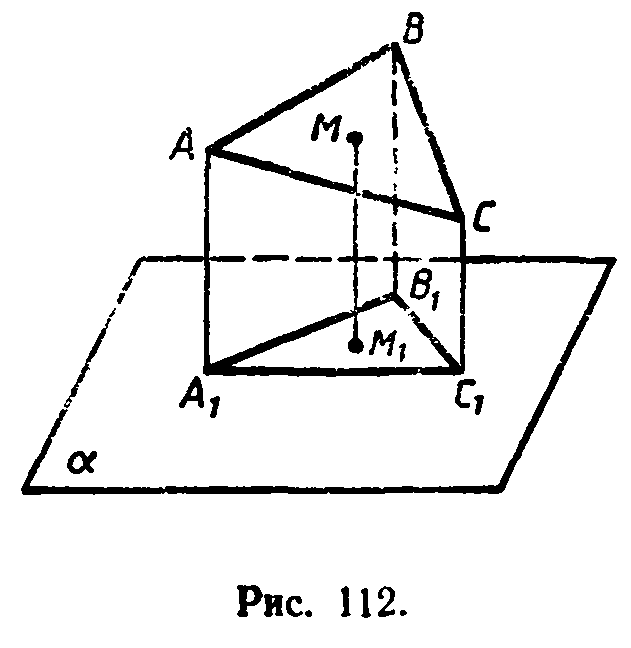
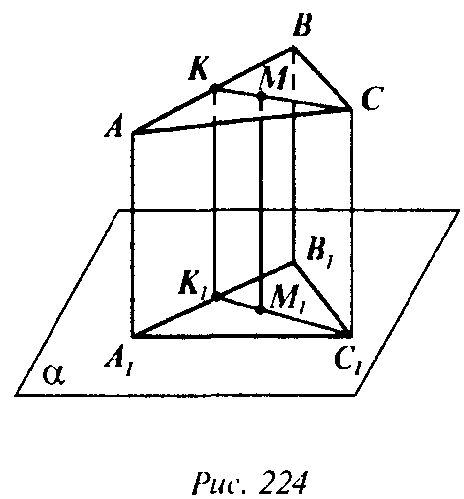
Глава IV. Векторы в пространстве § 3. Компланарные вектора → номер 373 373. Точки А1, В1, С1 и М1 —основания перпендикуляров, про веденных к плоскости α из вершин треугольника ABC и из точки М пересечения медиан этого треугольника (рис. 112). Останется ли верным равенство, если какие-то стороны треугольника ABC пересекаются с плоскостью α?
Докажите, что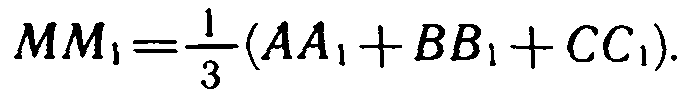 
Докажем, что M1 — точка пересечения медиан
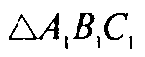
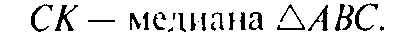
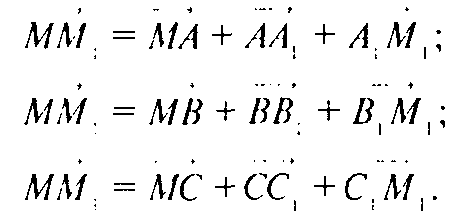
Сложив полученные равенства, учитывая, что
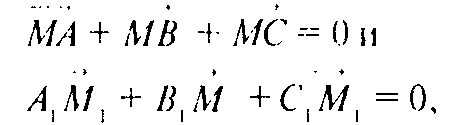
Получаем
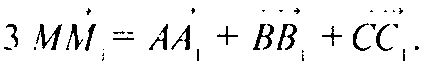
Так как векторы
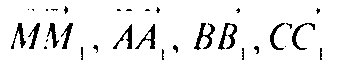
Сонаправлены, то
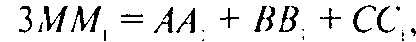
Ч. т. д. Если какие-то стороны ΔABC пересекаются с плоскостью α, то векторы ММ1, AA1, ВВ1, СС1, не будут сонаправлены, поэтому требуемое равенство не будет верно.