383. Числа k и l не равны друг другу. Докажите, что если векторы a+kb и a+lb не коллинеарны, то: а) векторы а и b не коллинеарны; б) векторы a+k1b и а+lb не коллинеарны при любых неравных числах k1 и l1

Глава IV. Векторы в пространстве Дополнительные задачи → номер 383

а) Предположим, что a и b коллинеарны. Тогда a = nb. Следовательно

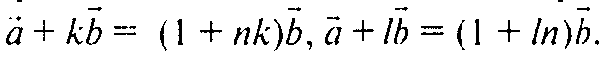
Но тогда

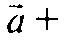
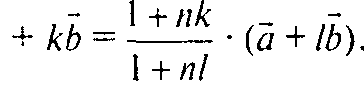
Т. е. вектора

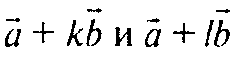
Коллинеарны, что противоречит условию. Значит a и b не коллинеарны. б) Если

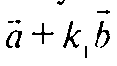
Коллинеарен

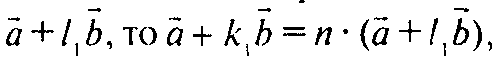
Тогда

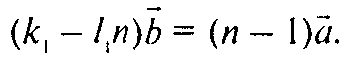
А это означает, что a и b коллинеарны, но тогда и a + kb и a + lb коллинеарны, что противоречит условию.