Глава I Параллельность прямых и плоскостей. §2 Взаимное расположение прямых в пространстве. Угол между двумя прямыми. → номер 40 40. На скрещивающихся прямых а и b отмечены соответственно точки М и N. Через прямую а и точку N проведена плоскость α, а через прямую b и точку М — плоскость β. а) Лежит ли прямая b в плоскости α? б) Пересекаются ли плоскости α и β? При положительном ответе укажите прямую, по которой они пересекаются.
А)
Скрещивающиеся прямые не лежат в одной плоскости. Следовательно,
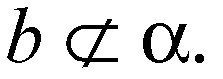
Б) α и β имеют две общие точки: М и N, значит, прямая MN — общая для плоскостей α и β, значит, это линия их пересечения (по аксиоме А2).
Ответ: а)
Б) MN — прямая, по которой плоскости α и β пересекаются.
