Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 406
Рассмотрим общий случай. Рассмотрим два некомпланарных вектора AB и DC. Перенесем вектор DC параллельно так, чтобы точка D1 его начала совпала с точкой В конца первого вектора. Получим вектор D1C1 или, что то же самое, вектор ВС1 сонаправленный с вектором DC и равный ему по длине. Согласно правилу сложения векторов:
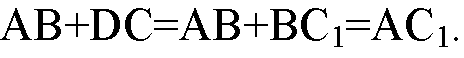
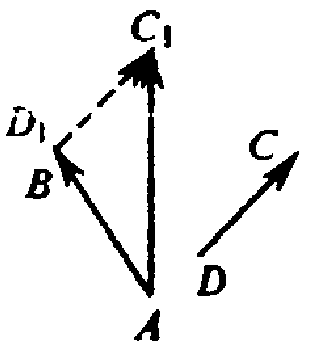
Пусть
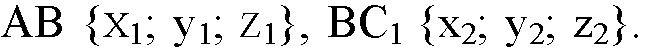
Докажем, что
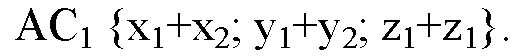
Для доказательства выразим координаты этих векторов через координаты
Их начала и конца.
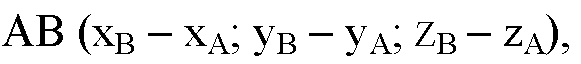
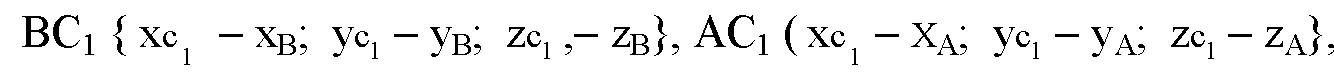
Из обозначения координат вектора AB как х1, у1 и z1 и вектора BC1 как x2, у2, z2, получим
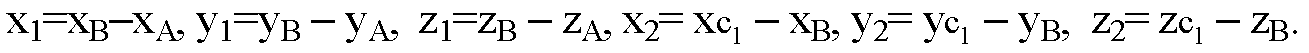
Вычислим суммы
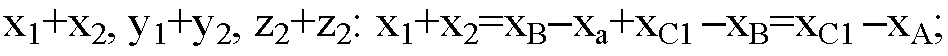
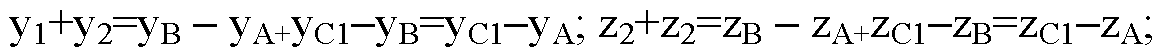
Суммы координат x1+x2, y1+y2, z1+z2 являются координатами вектора АС1 равного сумме исходных двух векторов AB и DC. Что и требовалось доказать.
