Глава I Параллельность прямых и плоскостей. §2 Взаимное расположение прямых в пространстве. Угол между двумя прямыми. → номер 43
* Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости.
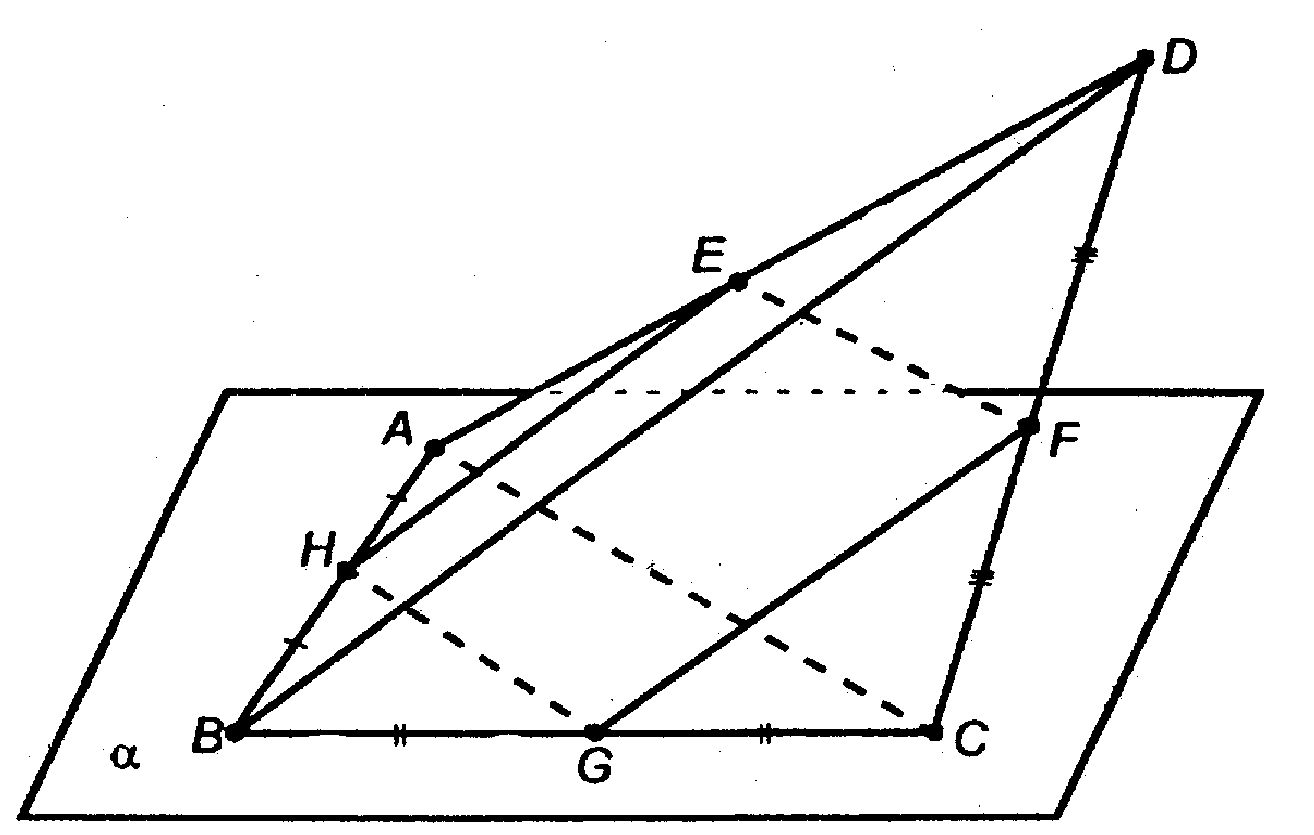
Соединим все вершины пространственного четырехугольника.
НЕ — средняя линия ΔBAD,
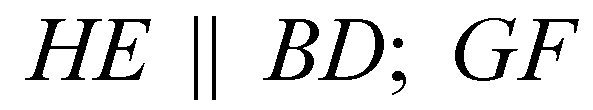
— средняя линия
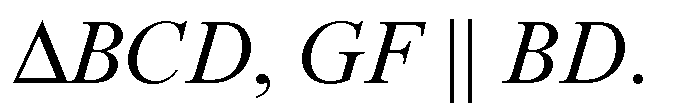
Значит,
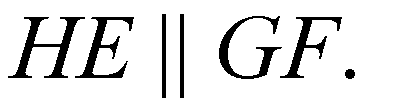
GH — средняя линия
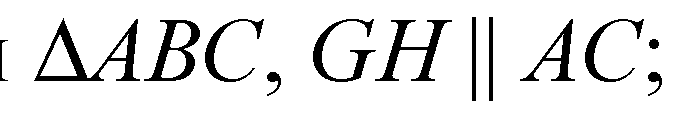
EF — средняя линия
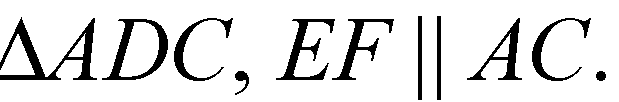
Отсюда
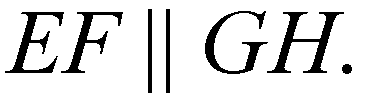
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом, следовательно, EFGH — параллелограмм (из параллельности сторон также следует, что четырехугольник плоский).
