Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 436
По формуле расстояния между двумя точками вычислим длины сторон трапеции A BCD:
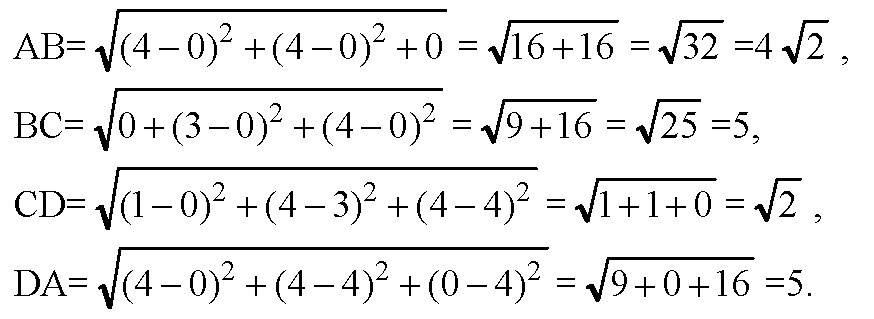
|AD|=|CB|=5, следовательно, ABCD будет равнобедренной трапецией, если доказать, что DC || AB, то есть, что DC и АВ коллинеарны.
Если существует число k такое, что
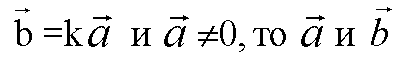
Коллинеарны.
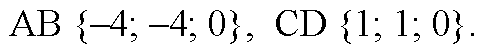
Очевидно, что АВ=-4CD, т. е. АВ и CD коллинеарны. значит, АВ || CD и ABCD — равнобедренная трапеция.
