Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов → номер 472
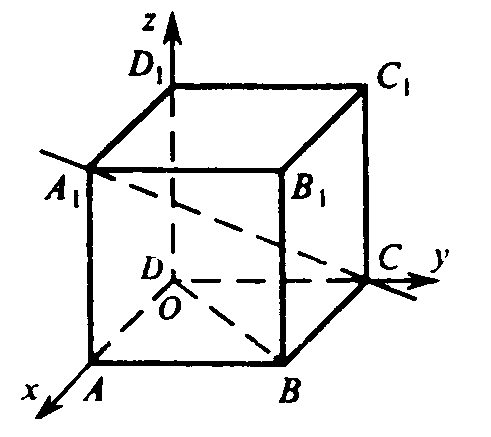
Введем прямоугольную систему координат. С началом координат в т. D и осями, направленными вдоль ребер ОА, ОВ, ОС. Обозначим сторону куба через а. Тогда:
1)
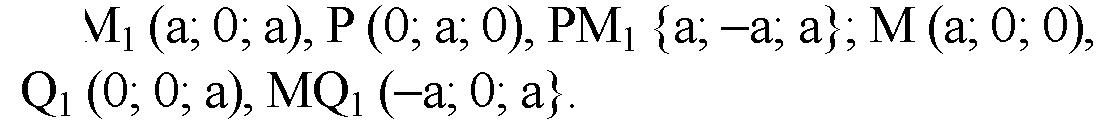
PM1 и MQ1 — направляющие векторы прямых PM1 и MQ1, угол между ними равен углу между этими прямыми.
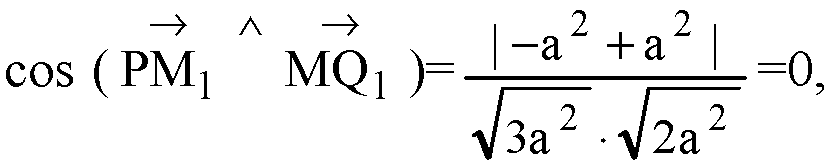
Следовательно, угол между прямыми
РМ1 и МQ1 равен 90°.
Докажем, что прямая MN1, пересекающая прямую MQ1 в точке М и лежащая в плоскости MN1Q1, перпендикулярна прямой РМ1.
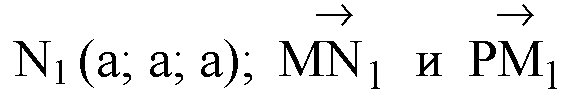
— направляющие векторы этих прямых.
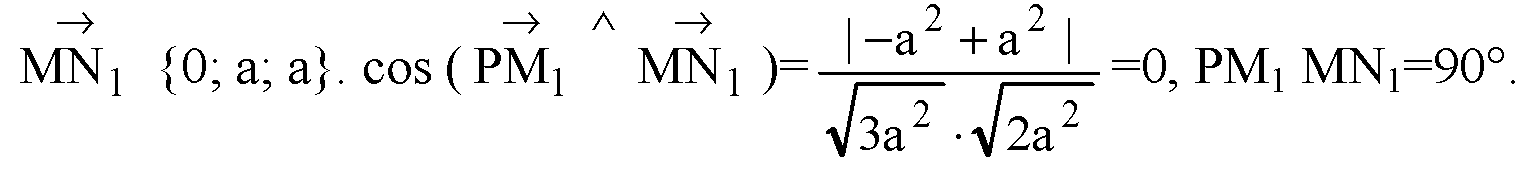
Доказали, что РМ1 ⊥ MQ1; РМ1 ⊥ MN1 лежит в плоскости MN1Q1; MN1 лежит в плоскости MN1Q1. Эти прямые пересекаются в точке М. Значит, РМ1 ⊥ плоскости MN1Q1.
2) Прямые QN и QP1 лежат в плоскости QNP1 и пересекаются в точке Q.
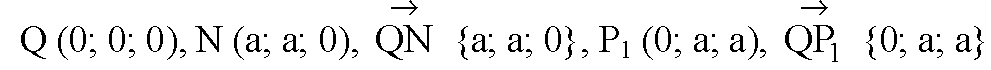
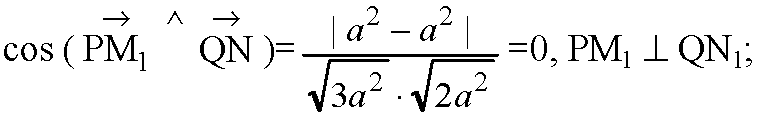
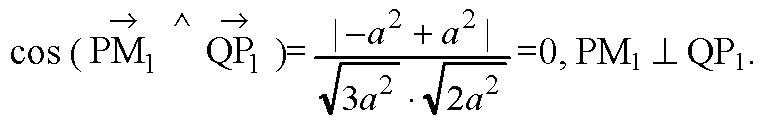
Таким образом, прямая РА1 ⊥ плоскости QNP1.
