Глава I Параллельность прямых и плоскостей. §3 Параллельность плоскостей → номер 56
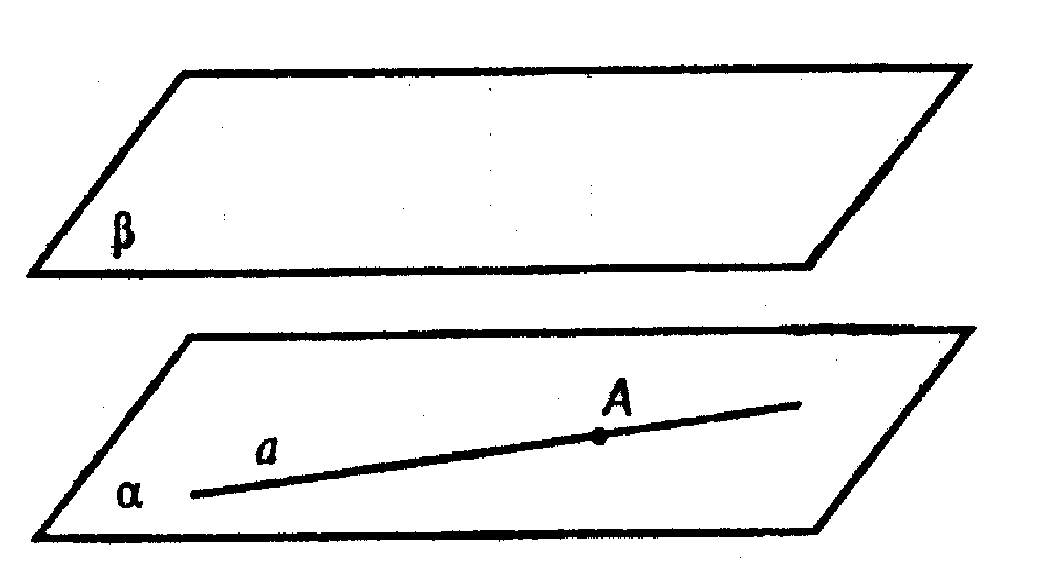
Пусть
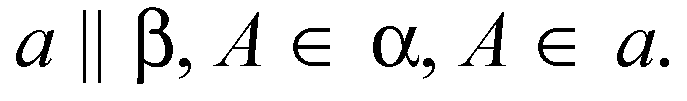
Докажем, что
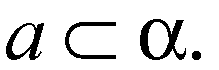
Мы знаем, что если некоторая прямая а пересекает плоскость α, то она пересекает также любую плоскость, параллельную α.
Если а не параллельна пл. β, то она пересекала бы пл. β, а, значит, и плоскость α, а по условию α || β.
Значит, а не может пересекать пл. α и, раз она имеет с пл. α общую точку А, то а ⊂ α.
