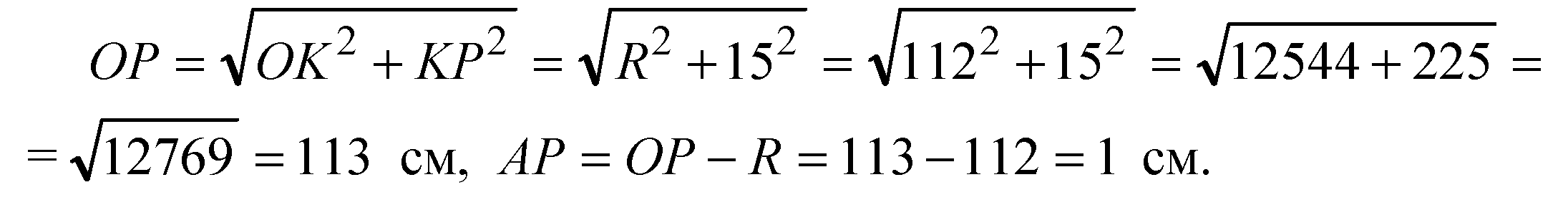Глава VI. Цилиндр, конус и шар § 3. Сфера → номер 592
а — касательная плоскость к сфере, P ∈ α, КР=15 см, ОК=ОА=R=112 см. Докажем, что точка A ∈ OP будет ближайшей точкой к точке Р.

Выберем произвольную точку N на сфере. Проведем отрезки NO и NP. По свойству сторон треугольника:
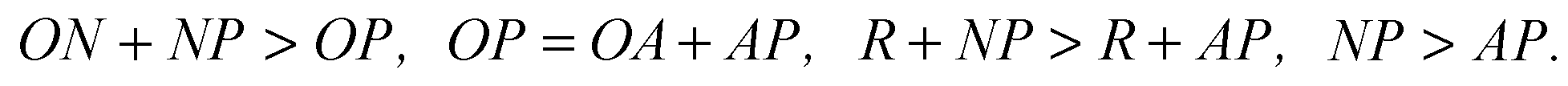
Итак, AP < NP, а далее так как точка N выбрана произвольно, то утверждение доказано. Из прямоугольного ΔОКР имеем: