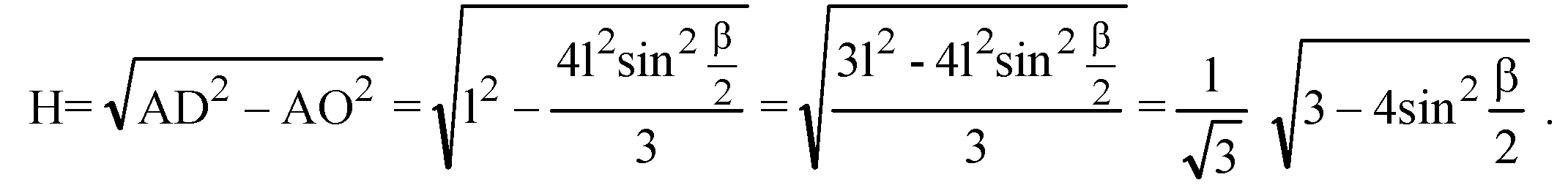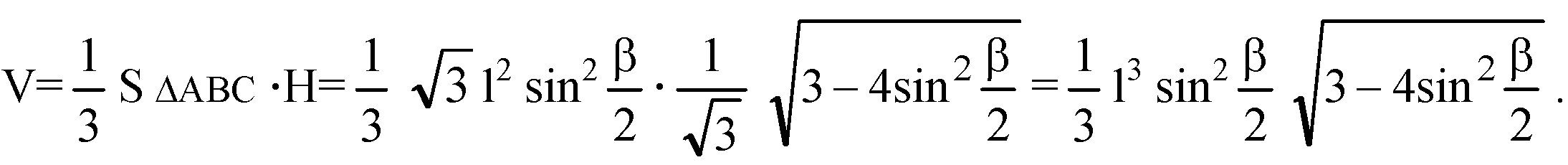Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса → номер 686 686. Найдите объем правильной треугольной пирамиды с боковым ребром l, если: а) боковое ребро составляет с плоскостью основания угол φ; б) боковое ребро составляет с прилежащей стороной основания угол α; в) плоский угол при вершине равен β.
а) DO — высота пирамиды.
Из прямоугольного треугольника ΔADO:
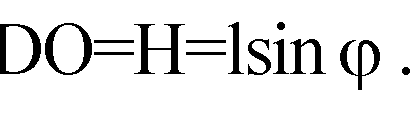
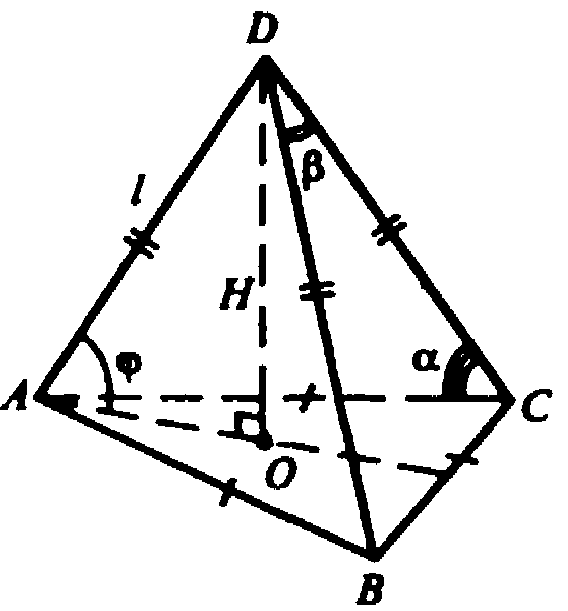
Точка О — центр ΔАВС, ОА — радиус описанной около ΔАВС окружности.
По теореме синусов:
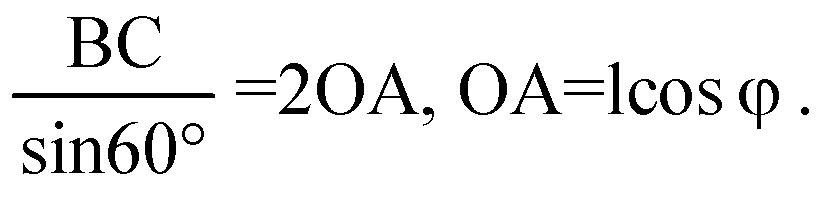
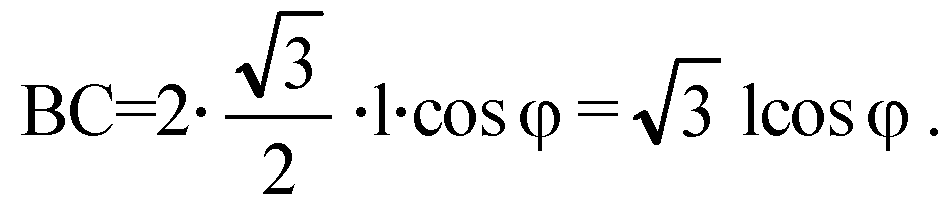
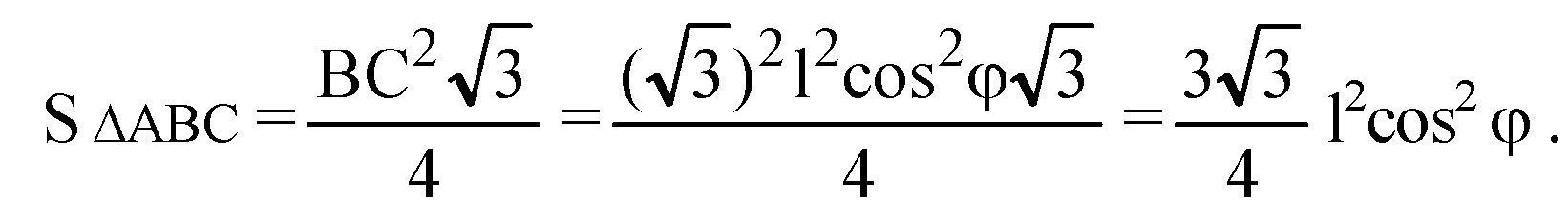
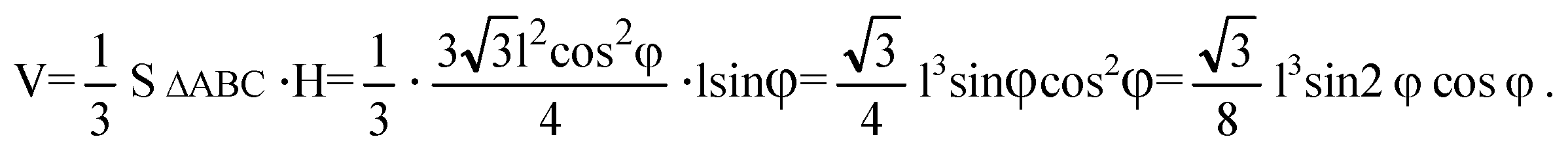
Б) ΔADC — равнобедренный.
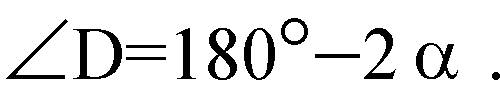
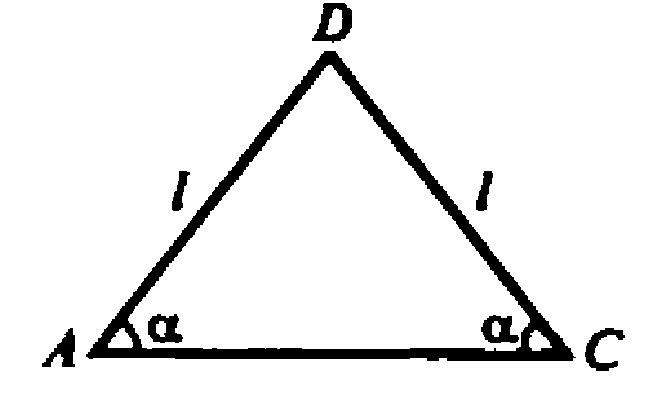
По теореме косинусов имеем:
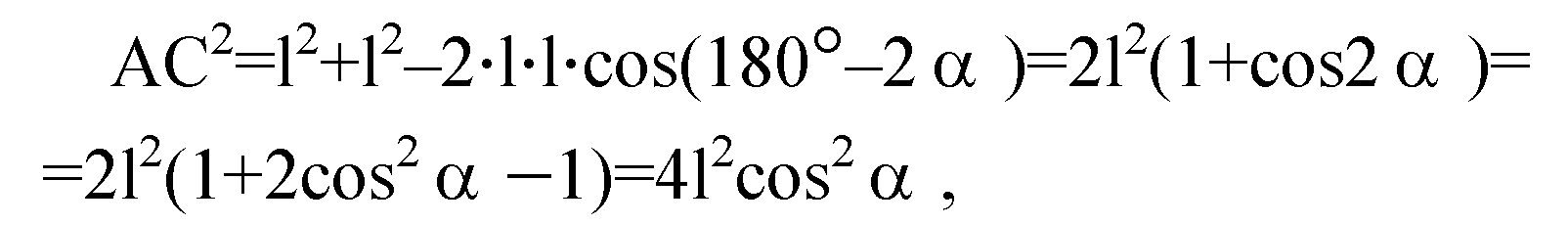
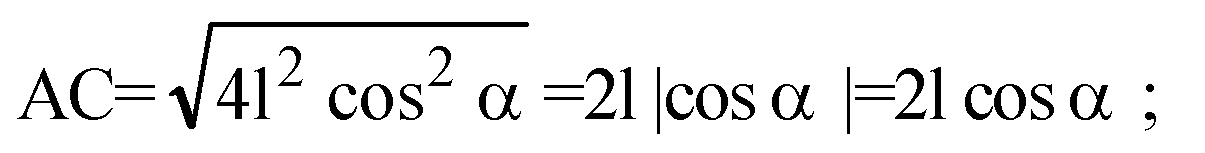
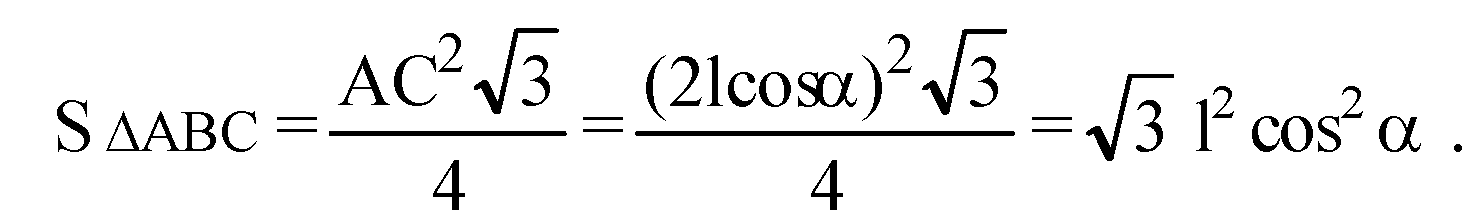
Вычислим длину отрезка ОА, ОА=R, где R — радиус окружности, описанной около ΔАВС.
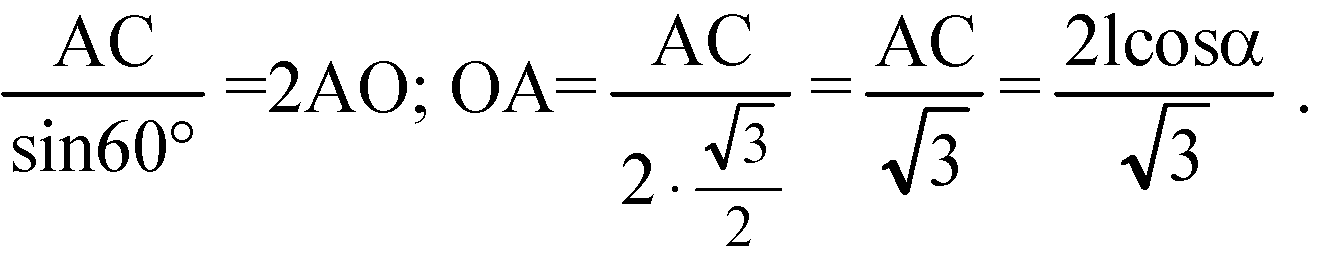
Из ΔADO:
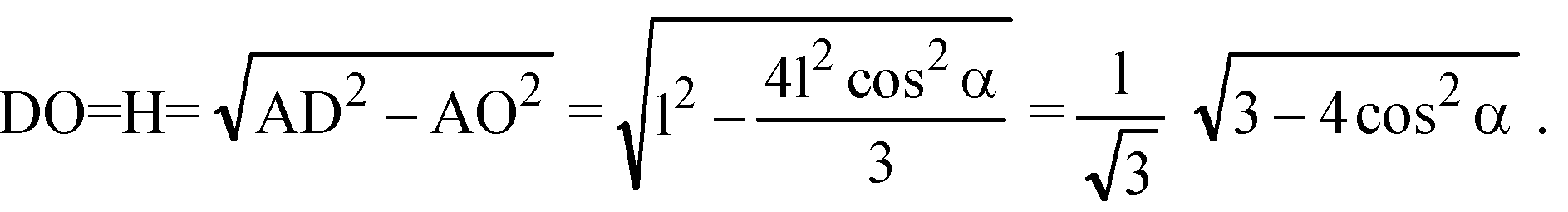
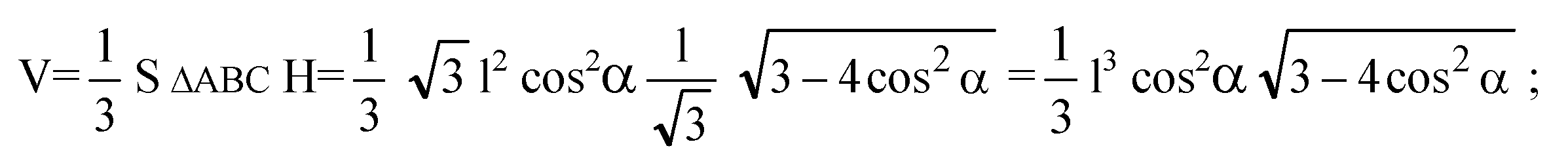
В) ΔBDC — равнобедренный. По теореме косинусов:
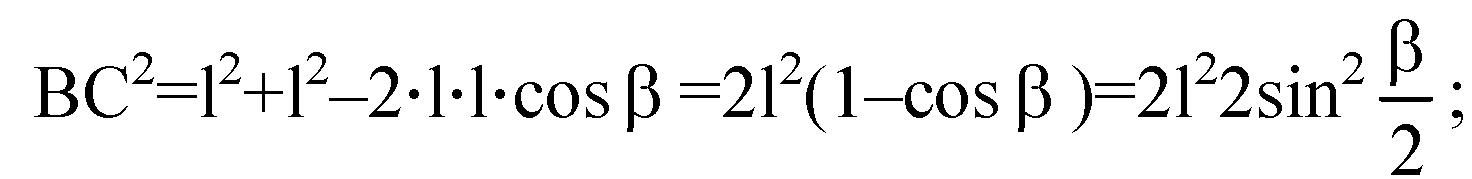
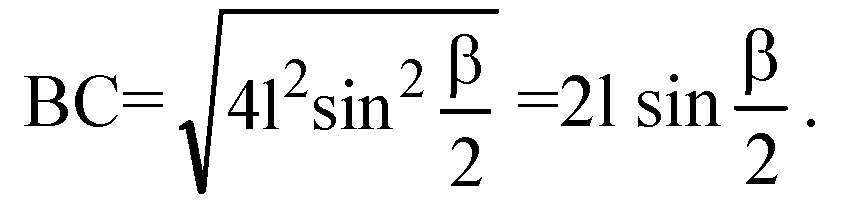
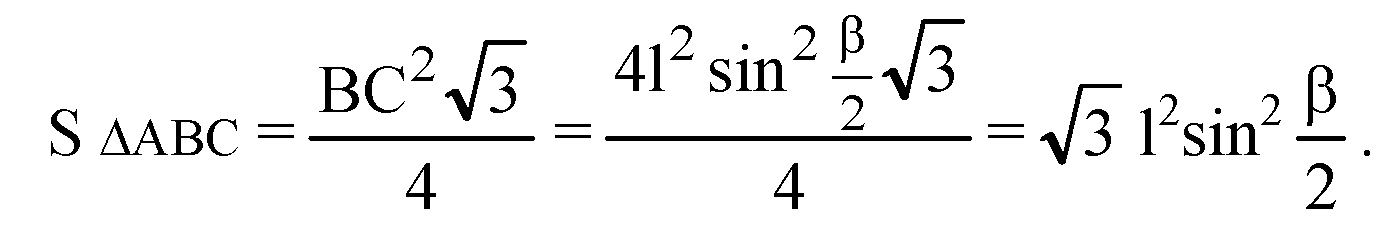
В треугольнике ΔАВС: ОА — радиус описанной окружности:
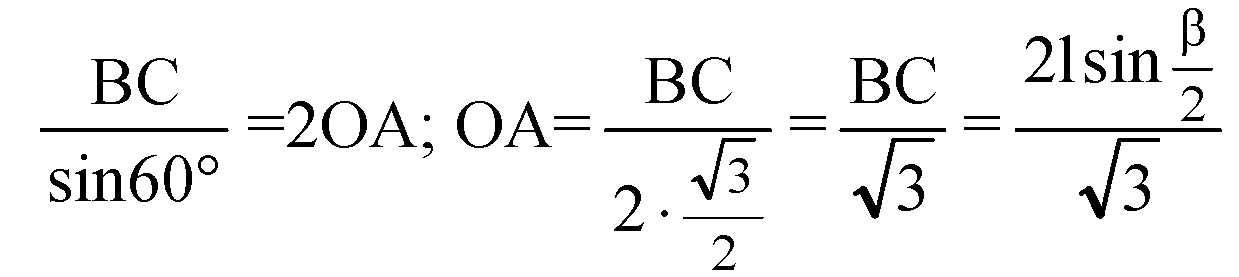
Из прямоугольного ΔAOD: