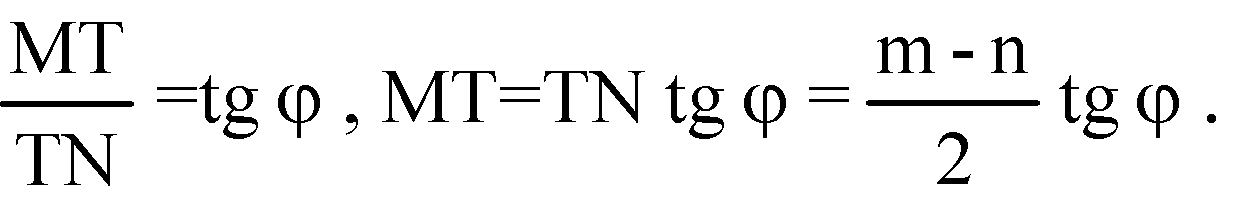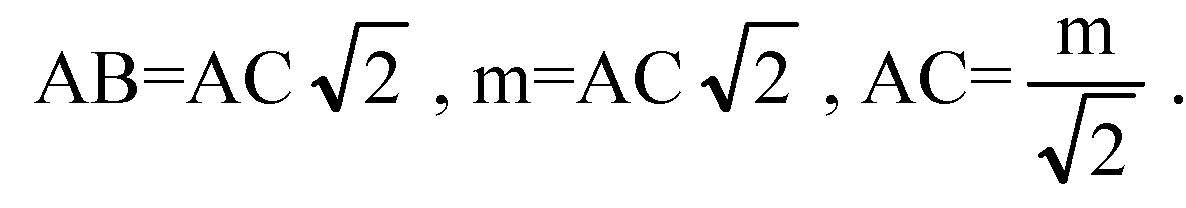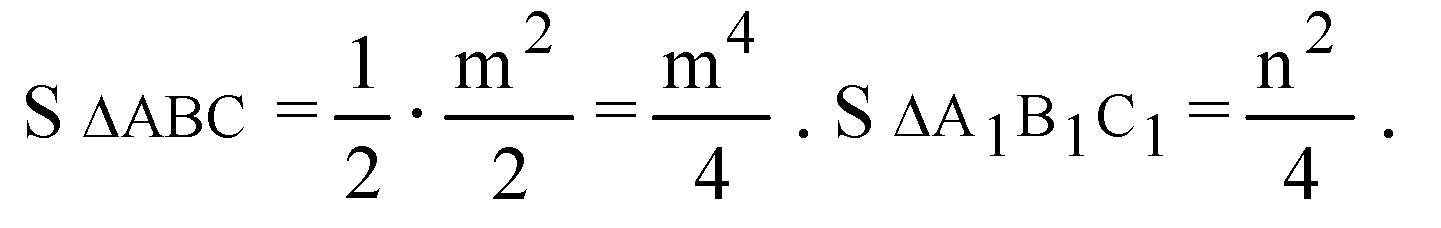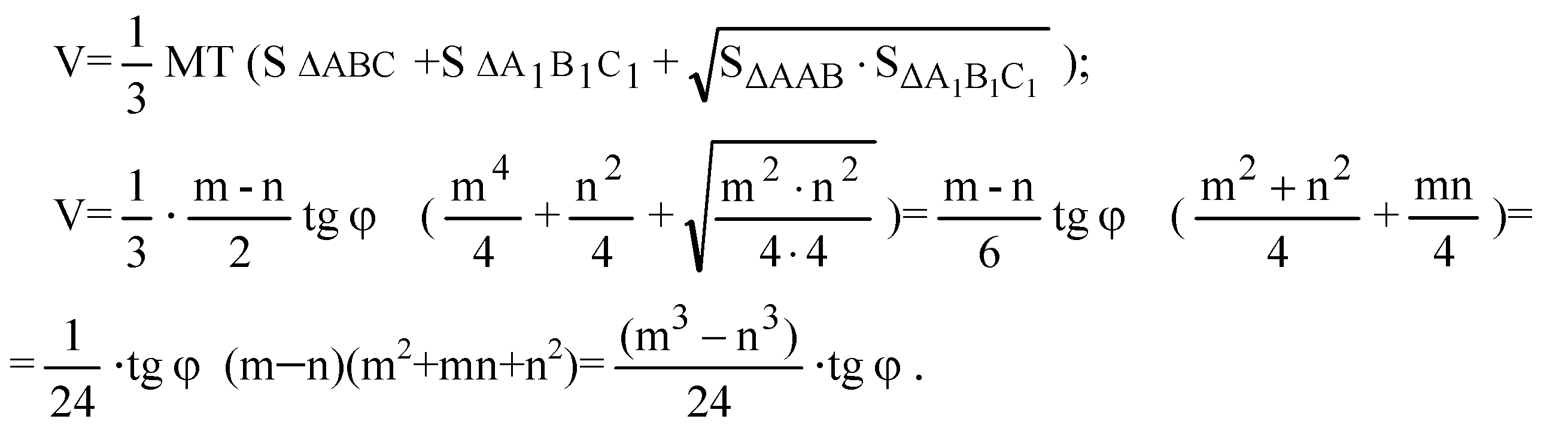Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса → номер 698 698. Основания усеченной пирамиды — равнобедренные прямоугольные треугольники, гипотенузы которых равны m и n (m>n). Две боковые грани, содержащие катеты, перпендикулярны к основанию, а третья составляет с ним угол φ. Найдите объем усеченной пирамиды.
Построим С1М⊥А1В1 и CN⊥AB, отрезок MN. Т. к. АВ⊥CN и АВ⊥С1С, то плоскость С1CNM⊥AB, MN⊥AB, MN — апофема. Проведем МТ⊥CN, МТ — высота пирамиды. ∠MNT= φ — линейный угол двугранного угла МАВС.
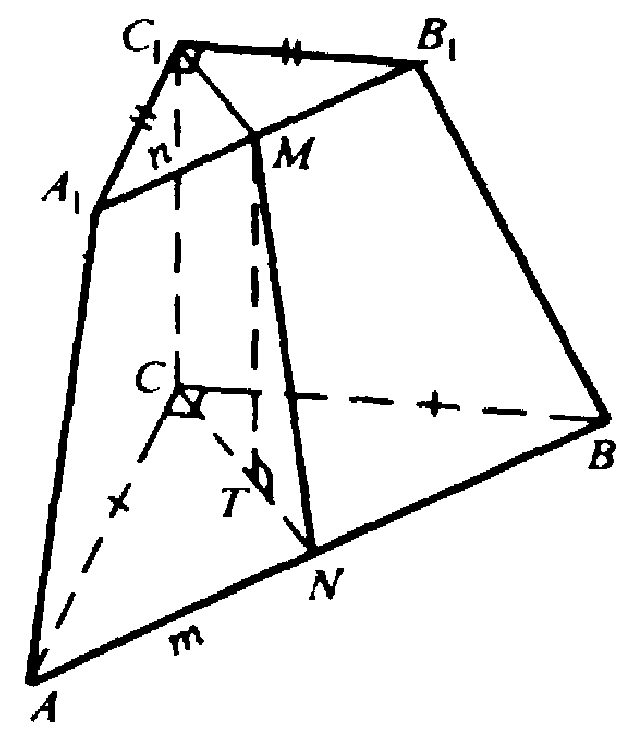
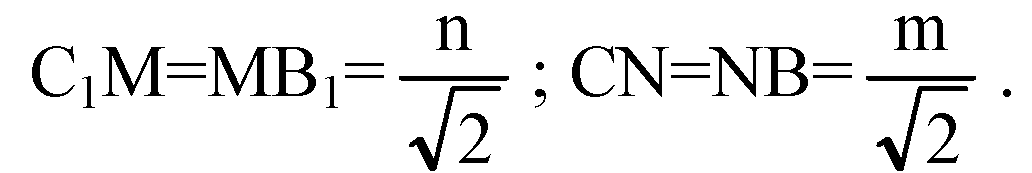
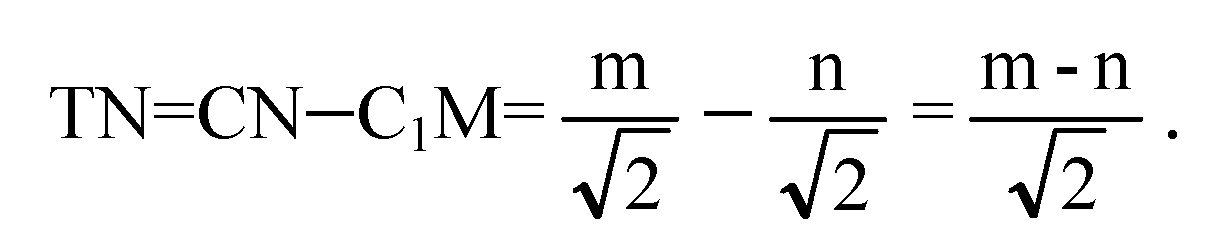
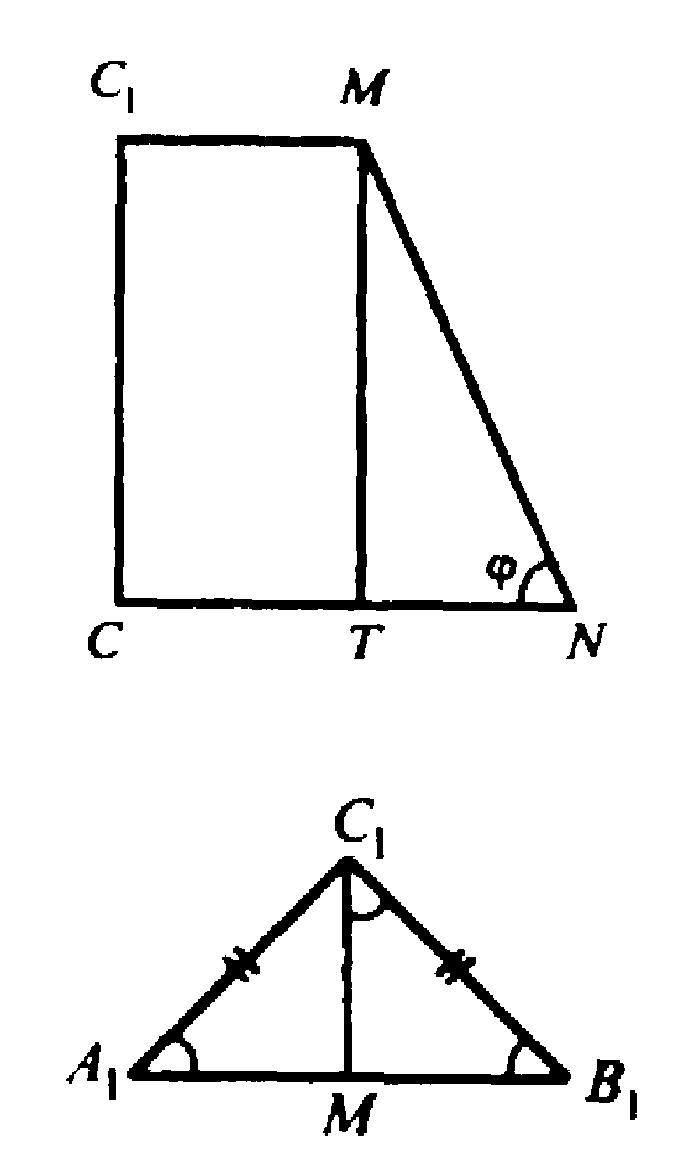
В ΔМТN: