Дополнительные задачи к главе VII → номер 734 734. На трех данных параллельных прямых, не лежащих в одной плоскости, отложены три равных отрезка АА1, ВВ1 и СС1. Докажите, что объем призмы, боковыми ребрами которой являются эти отрезки, не зависит от положения отрезков на данных прямых.
х||у||z, AA1=BB1=CC1. Известно (см. задачу 733), что объем треугольной призмы равен половине произведения площади боковой грани на расстояние от этой грани до параллельного ей ребра.
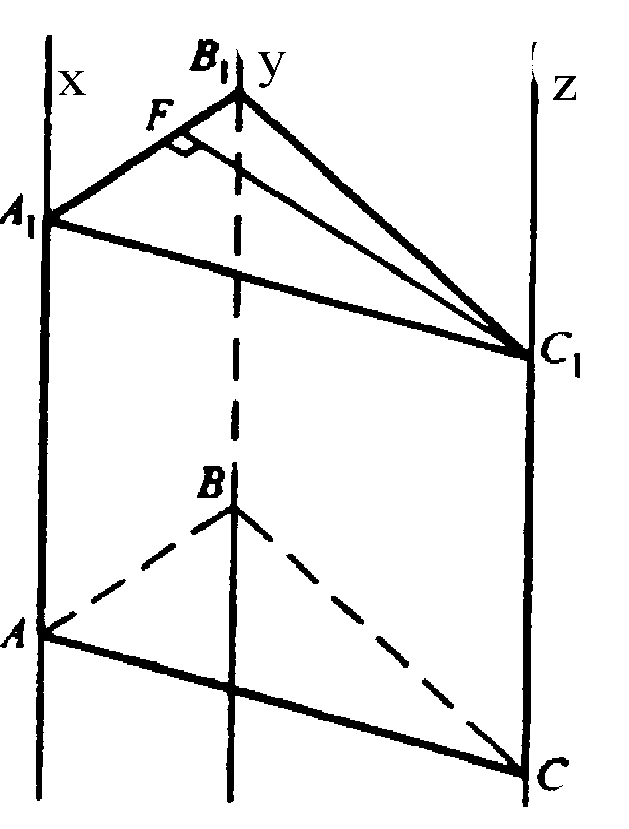
Возьмем за основание грань АА1В1В, из точки С1
Проведем отрезок C1F ⊥ плоскости АА1В1В. Отрезок C1F — высота призмы.
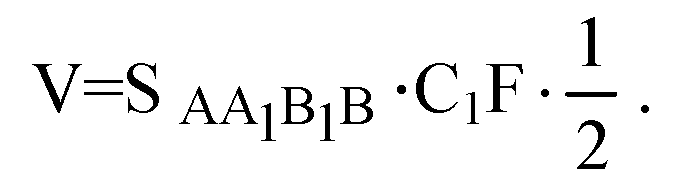
Длина C1F — величина постоянная при заданном положении x, y, z. Расстояние между параллельными прямыми x и y, а значит, и между отрезками АА1 и ВВ1 не меняется, тогда, высота параллелограмма АА1В1В — величина постоянная. Тогда площадь S AA1B1B =const, значит V=const.
