Задачи повышенной трудности → номер 772
Данные точки являются вершинами тетраэдра. Они не могут лежать все по одну сторону от искомой плоскости, тогда как они лежали бы в одной плоскости, параллельной этой плоскости. Аналогично ни одна из них не лежит в искомой плоскости. Поэтому возможны лишь два случая:
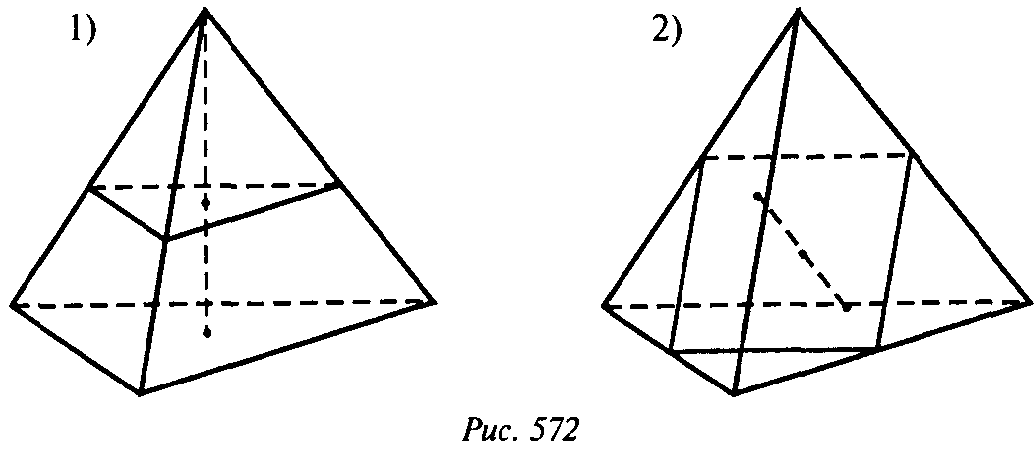
1) По одну сторону от искомой плоскости лежат три данные точки, по другую — одна. Плоскость походит через середины ребер тетраэдра, исходящих из одной вершины. Расстояния равны половине высоты тетраэдра, исходящей из этой точки.
2) По одну сторону от плоскости две точки, по другую — также две. Плоскость проходит через середины ребер, исходящих из двух
Вершин. Расстояния равны половине расстояния между скрещивающимися ребрами, то есть расстоянию между параллельными плоскостями, проходящими через эти ребра.
Первому условию удовлетворяют четыре плоскости, второму — три; всего имеем семь плоскостей.
