Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 82 82. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте внутреннюю точку М грани АА1В1В. Постройте сечение параллелепипеда, проходящее через точку М параллельно: а) плоскости основания ABCD; б) грани ВВ1С1С; в) плоскости BDD1.
А)
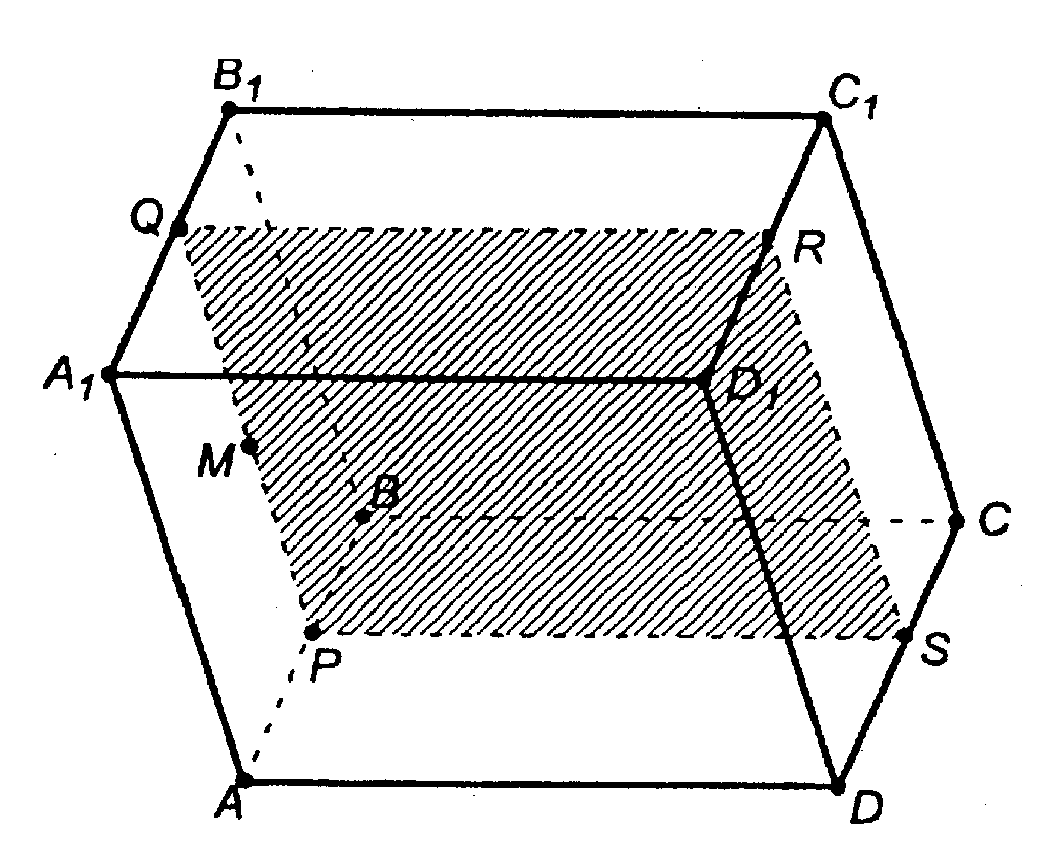
Построение
Плоскость сечения по условию || пл. ABCD, следовательно, она пересекает грани параллелепипеда по прямым, параллельным АВ, DC, BC и AD (это следует из теоремы II). Отсюда способ построения:
1. через т. М проводим PQ || AB;
2. через т. Q проводим QR || BC;
3. через т. Р проводим PS || AD;
4. соединим точки S и R;
PQSR — искомое.
Б)
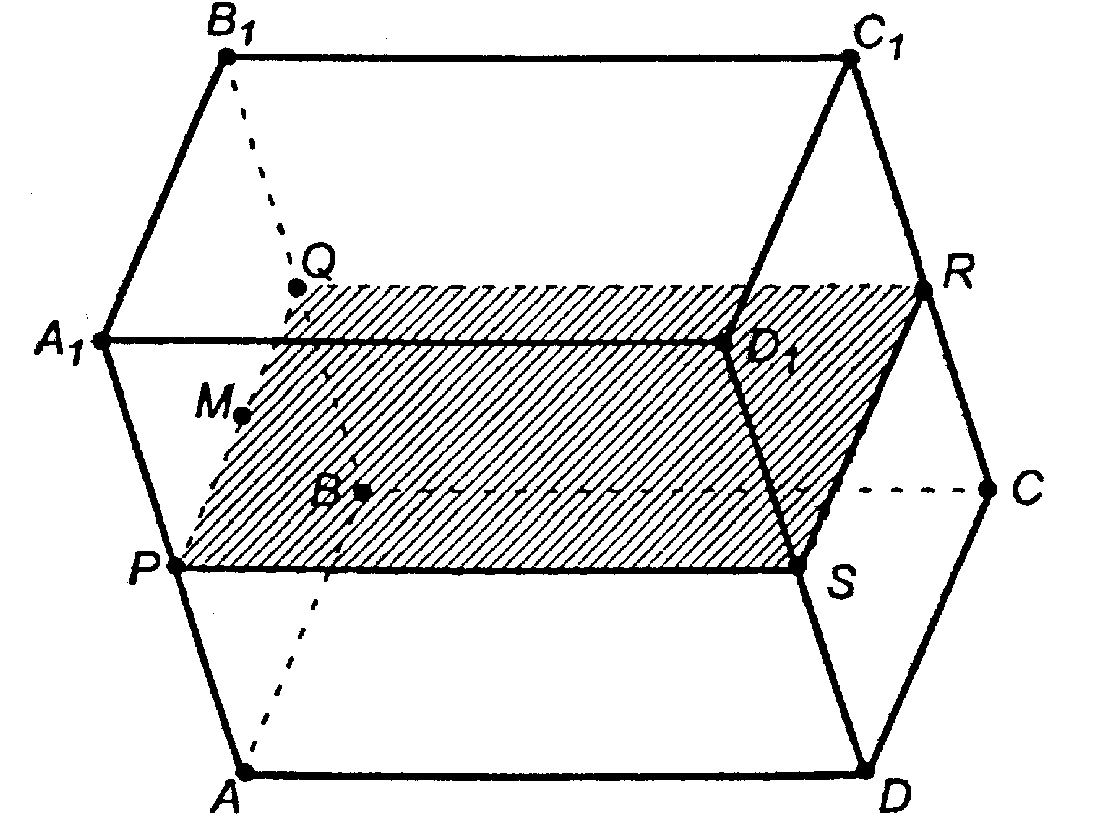
По теореме II, плоскость сечения пересечет боковые грани по прямым, параллельным АА1 и DD1, а плоскости оснований — по прямым, параллельным A1D1 и AD. Отсюда:
1. через т. М проводим PQ || AA1;
2. через т. Q проводим QR || A1D1 и через т. Р проводим PS || AD;
3. соединим точки R и S;
4. сечение PQRS — искомое.
В)
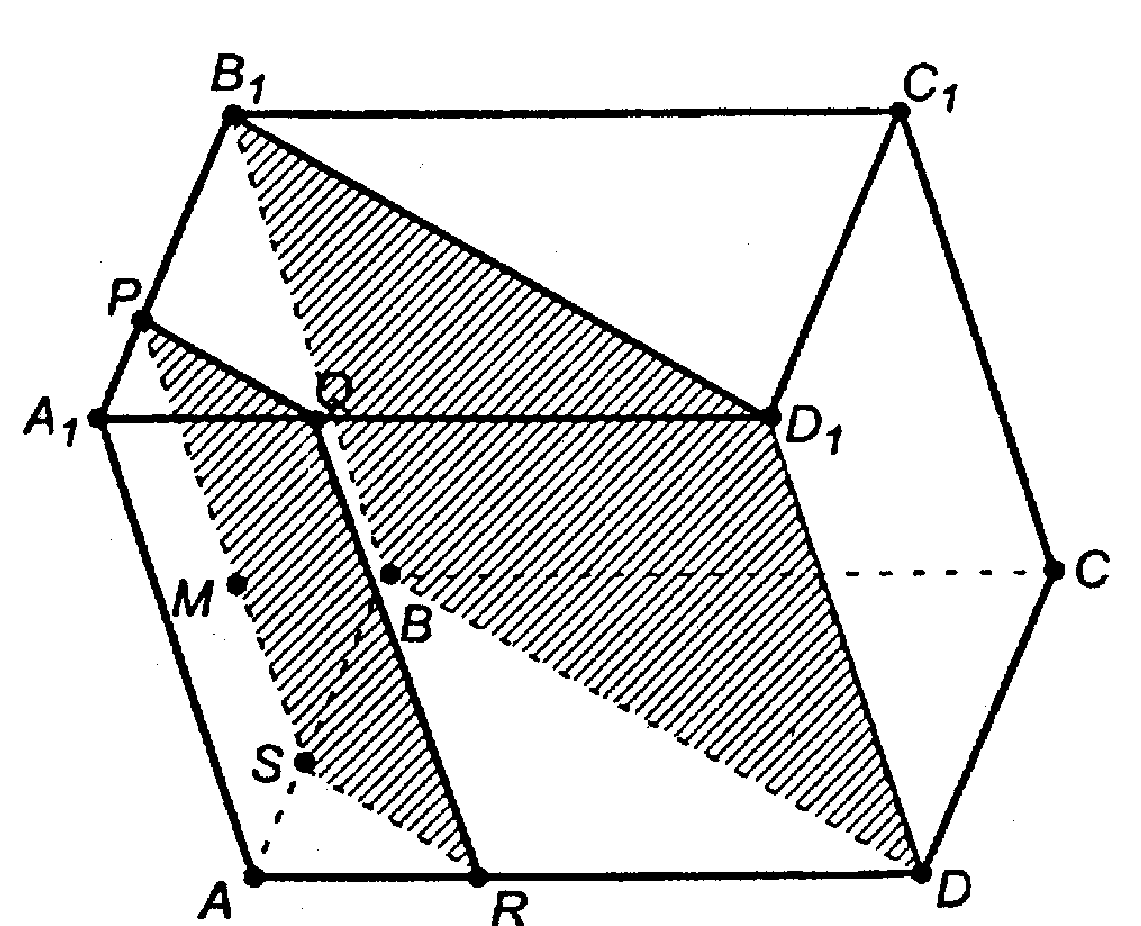
1) Построим плоскость BDD1; она пересечет плоскости верхнего и нижнего основания по параллельным прямым. BD || B1D1 (соединив В1 и D1, получим параллелограмм BB1D1D).
2) Плоскость сечения по условию параллельна пл. BB1D1D, значит, она параллельна BB1D1D.
По теореме II получим, что если плоскость боковой грани АА1В1В проходит через прямую ВВ1, а ВВ1 параллельна плоскости сечения и пересекает плоскость сечения, то линия пересечения боковой грани с сечением параллельна прямой В1В, получим построение:
1. через т. М проводим PS || B1B;
2. через т. Р проводим PQ || B1D1;
3. через т. S проводим SR || BD;
4. соединим т. Q и т. R;
5. сечение PQRS — искомое сечение.
