Глава III Многогранники. § 3. Правильные многогранники
1. Какое наименьшее число ребер может иметь многогранник?
1. Наименьшее число ребер имеет тетраэдр — 6.
2. Призма имеет п граней. Какой многоугольник лежит в ее основании?
(n — 2) — угольник.
3. Является ли призма прямой, если две ее смежные боковые грани перпендикулярны к плоскости основания?
Да, является.
4. В какой призме боковые ребра параллельны ее высоте?
В прямой призме.
5. Является ли призма правильной, если все ее ребра равны друг другу?
Нет, она может быть и не прямой.
6. Может ли высота одной из боковых граней наклонной призмы являться и высотой призмы?
Да, если эта грань перпендикулярна основаниям.
7. Существует ли призма, у которой: а) боковое ребро перпендикулярно только одному ребру основания; б) только одна боковая грань перпендикулярна к основанию?
а) да. б) нет.
8. Правильная треугольная призма разбивается плоскостью, проходящей через средние линии оснований, на две призмы. Как относятся площади боковых поверхностей этих призм?
По теореме п. 27 получаем, что боковые поверхности относятся, как 5 : 3
9. Будет ли пирамида правильной, если ее боковыми гранями являются правильные треугольники?
Да
10. Сколько граней, перпендикулярных к плоскости основания, может иметь пирамида?
Две.
11. Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?
Нет, иначе бы через вершину пирамиды проходили бы как минимум две прямые, перпендикулярные основаниям.
12. Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?
. Да (рис 183).
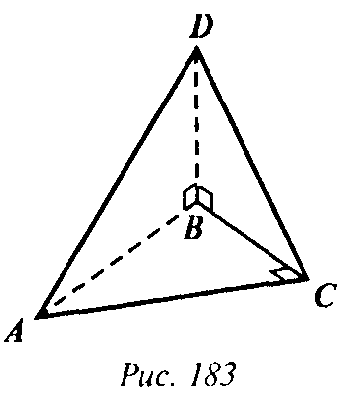
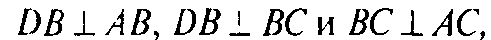
Тогда
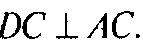
13. Можно ли из куска проволоки длиной 66 см изготовить каркасную модель правильной четырехугольной пирамиды со стороной основания, равной 10 см?
Нет, так как длина каркаса по крайней мере
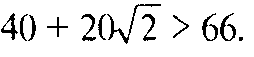
14. На какие многогранники рассекается треугольная призма плоскостью, проходящей через вершину верхнего основания и противолежащую ей сторону нижнего основания?
На тетраэдр и четырехугольную пирамиду.
