145 Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружности. Найдите ∠POM

Глава II. Треугольники. §4 Задачи на построение → номер 145

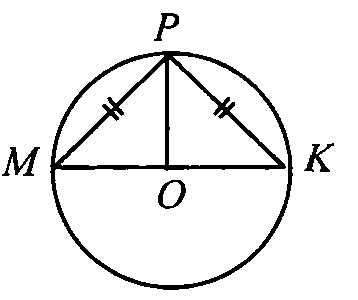
Из МР = РК следует, что ΔМРК — равнобедренный. Т. к. МО = ОК — радиусы, то РО — медиана равнобедренного ΔMPK, опущенная на основание, тогда РО — биссектриса и высота (по свойству равнобедренного треугольника) и ∠MOP = 90°.