Глава II. Треугольники. §4 Задачи на построение → номер 153
Построение приведено в учебнике.
Решение
Построим окружность с центром в данной точке М, пересекающую данную прямую а в двух точках, которые обозначим буквами А и B (рис. 91).
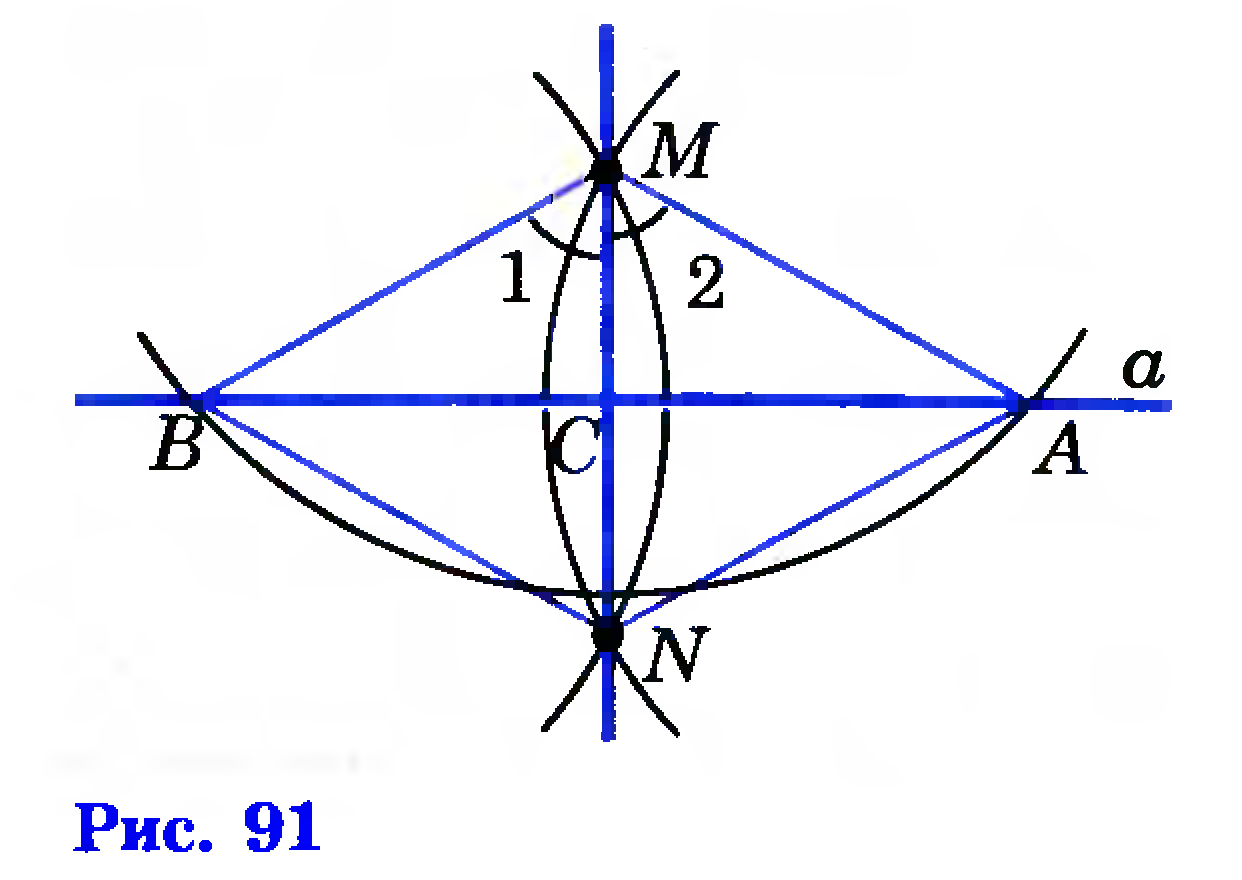
Затем построим две окружности с центрами А и B, проходящие через точку М. Эти окружности пересекаются в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую MN и докажем, что эта прямая — искомая, т. е. она перпендикулярна к прямой а.
В самом деле, треугольники AMN и BMN равны по трем сторонам, поэтому ∠1=∠2. Отсюда следует, что отрезок МС (С — точка пересечения прямых а и MN) является биссектрисой равнобедренного треугольника АМB, а значит, и высотой. Таким образом, MN ⊥ AB, т. е. MN ⊥ а.
