221 Даны треугольник ABC и точки М и N такие, что середина отрезка ВМ совпадает с серединой стороны АС, а середина отрезка CN — с серединой стороны AB. Докажите, что точки М, N и А лежат на одной прямой

Глава III. Параллельные прямые. §2 Аксиома параллельных прямых → номер 221

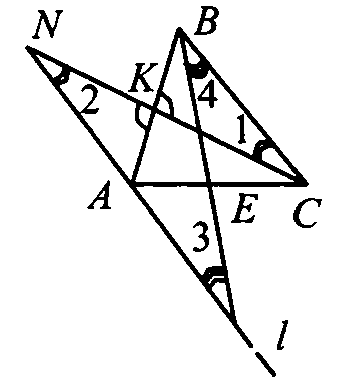
ΔВСК = ΔANK по первому признаку (АК = KN, NK = СК, ∠AKN = ∠CKB — вертикальные). Значит ∠1 = ∠2.

ΔВЕС = ΔМЕА по первому признаку (АЕ = ЕС, BE = ЕМ, ∠BEC = ∠MEA — вертикальные). Значит ∠3 = ∠4.

∠1 и ∠2- накрест лежащие углы при прямых AN и ВС и секущей NC. Следовательно AN || ВС (1).

∠3 и ∠4 — накрест лежащие углы при прямых AM и ВС и секущей ВМ. Следовательно АМ || ВС (2).

Сравнивая (1) и (2), получим АМ || ВС и AN || ВС, значит AM || AN. Но прямые AM и AN проходят через одну точку А и параллельны одной и той же прямой ВС, то, по аксиоме параллельных прямых, можно утверждать, что AM и AN совпадают, т. е. A, N,M ∈ l, ч. т.д.