Глава IV. Соотношения между сторонами и углами треугольника. §1 Сумма углов треугольника → номер 231
— равнобедренные, тогда
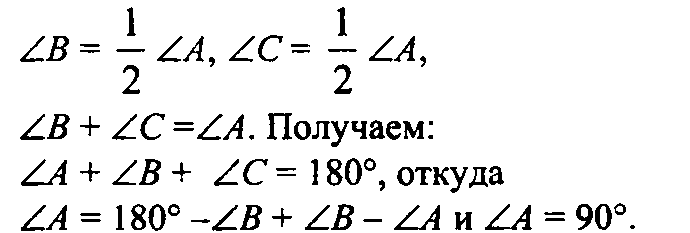
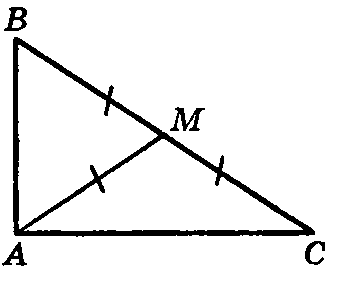
Пояснение:
По условию, BM=MC=AM. Построим точку D на продолжении AM за BC, при этом DM=AM. Тогда в четырехугольнике ABDC диагонали равны и в точке пересечения делятся пополам. Тогда это прямоугольник, а угол A будет прямым, что и требовалось.
