311 Что представляет собой множество всех точек плоскости, каждая из которых равноудалена от двух данных пересекающихся прямых?

Глава IV. Соотношения между сторонами и углами треугольника. §4 Построение треугольника по трем элементам → номер 311

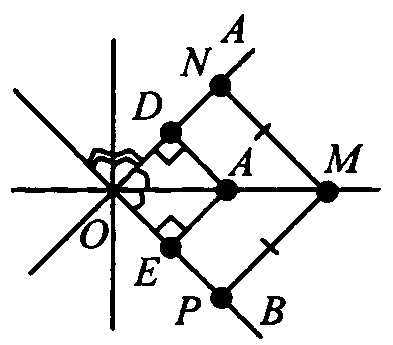
Построим биссектрисы углов, образованных при пересечении ОА и ОВ. Возьмем любую точку С на биссектрисе. Тогда ΔODC = ΔОЕС (ОС — общая гипотенуза и ∠1 = ∠2).

Значит CD = СЕ. Построим перпендикуляры MN и МР к ОА и ОВ.

Тогда ΔONM= ΔОРМ, т. к. ОМ — общая гипотенуза, MN = МР (по условию М равноудалена от ОА и ОВ).

Значит ∠NOM= ∠POM, т. е. ОМ-биссектриса ∠AOB. Значит искомое множество — это две прямые, являющиеся биссектрисами углов, образованных при пересечении данных прямых.