327 Даны шесть точек. Известно, что прямая, проходящая через любые две точки, содержит по крайней мере еще одну из данных точек. Докажите, что все эти точки лежат на одной прямой

Задачи повышенной трудности. Задачи к главе I → номер 327

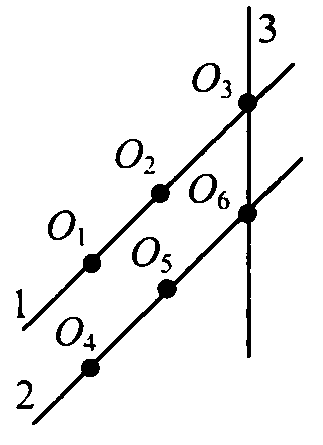
Из условия задачи следует, что наши шесть точек можно разбить на две тройки: пусть прямая 1 проходит через точки О1, O2 и О3, а прямая 2 проходит через точки O4, O5 и O6. Докажем, что прямые 1 и 2 совпадают: предположим противное. Тогда через точки О3 и О6 проходит прямая 3, и, поскольку две несовпадающие прямые могут пересекаться на плоскости только в одной точке, то точки O1, O2, O4 и O5 не принадлежат прямой 3, что противоречит условию, следовательно прямые 1 и 2 совпадают, и все шесть точек лежат на одной прямой.