Задачи повышенной трудности. Задачи к главам III и IV → номер 347
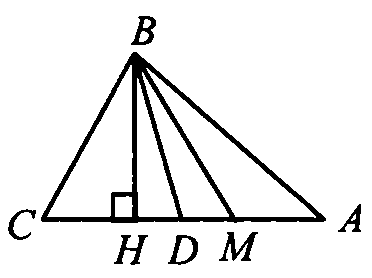

Не ограничивая общности, будем считать, что ВС < АВ, тогда, по доказанному в задаче № 346, получим, что точка Н принадлежит лучу DC.
По доказанному в задаче № 341, получим, что AD > DC, но
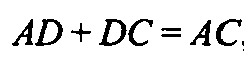
Следовательно,
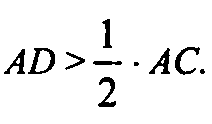
ВМ — медиана,
Следовательно,
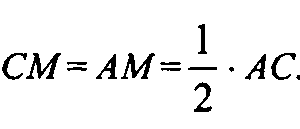
Получаем, что
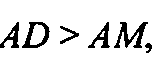
Т. е. точка М принадлежит отрезку AD, следовательно, точка М принадлежит отрезку AD, следовательно, точка М принадлежит лучу DA, а точка D лежит между точками H и М, ч. т.д.
