№ 58. Докажите, что геометрическое место вершин углов с заданной градусной мерой, стороны которых проходят через две данные точки, а вершины лежат по одну сторону от прямой, соединяющей эти точки, есть дуга окружности сконцами в этих точках. Пусть AB —

§11. Подобие фигур → номер 58

От прямой AB, равны 1/2 ∠AOB, поэтому они равны между собой.

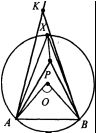
Докажем теперь, что данным свойством обладают только точки этой части окружности. Рассмотрим два варианта:

А) вершина Р лежит внутри окружности, тогда ∠APB > ∠AXB;

Б) вершина K лежит вне окружности, тогда ∠AXB > ∠AKB. Так что вершины должны лежать на окружности, то есть на

Дуге окружности.

Что и требовалось доказать.