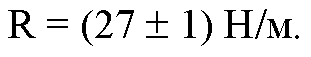ЛАБОРАТОРНЫЕ РАБОТЫ → номер 2
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
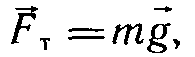
Уравновешивающей силу упругости на основе закона Гука:
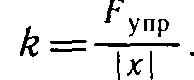
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости Fупр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
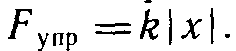
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины kср.
Результат измерения обычно записывается в виде выражения k = = kcp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (εk) равна отношению абсолютной погрешности Δk к значению величины k:
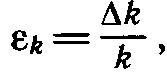
Откуда Δk — εkk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
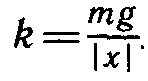
Поэтому
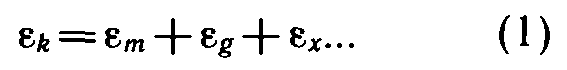
Средства измерения: 1) набор грузов, масса каждого равна m0 = 0,100 кг, а погрешность Δm0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
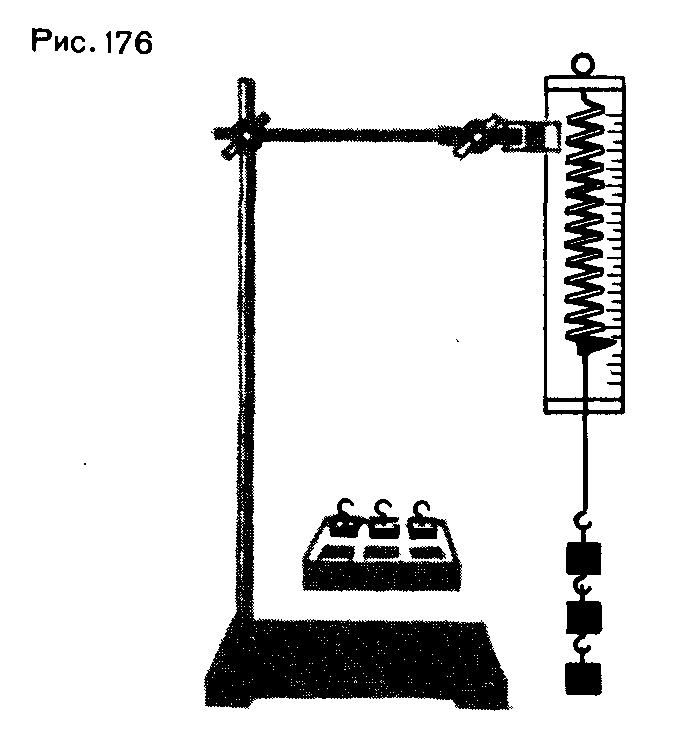
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
Номер
Опыта
M, кг
Mg1, Н
|х|, м
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kcp.
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение kср (из опыта с одним грузом). В формуле (1)
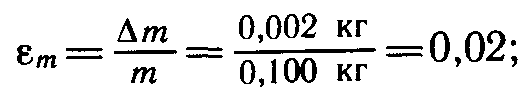
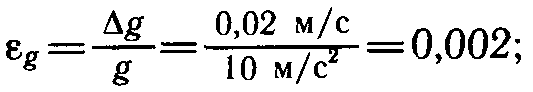
Так как погрешность при измерении удлинения Δx=1 мм, то

8. Найдите
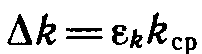
И запишите ответ в виде:
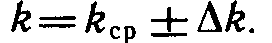
1 Принять g≈10 м/с2.
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
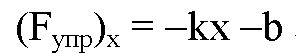
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
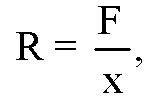
Где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
№ опыта
Масса, кг
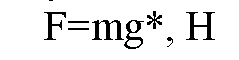
Удлинение |х|,
К, Н/м
М
1
0,1
1
0,036
27,78
2
0,2
2
0,074
27,03
3
0,3
3
0,112
26,79
4
0,4
4
0,155
25,81
* Ускорение свободного падения примем равным 10 м/с2.
Вычисления:
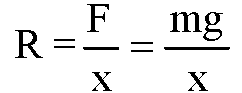
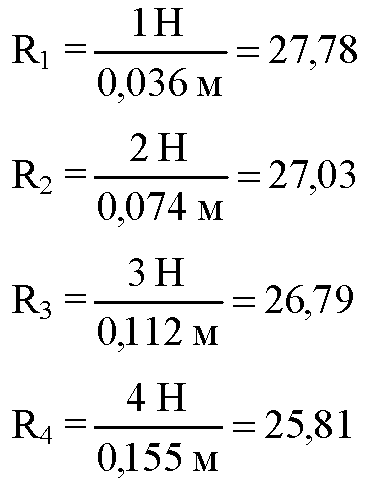
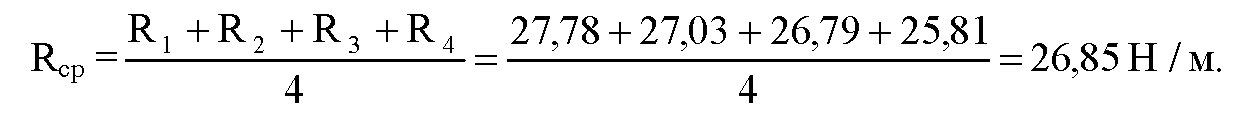
Вычисление погрешности измерения:
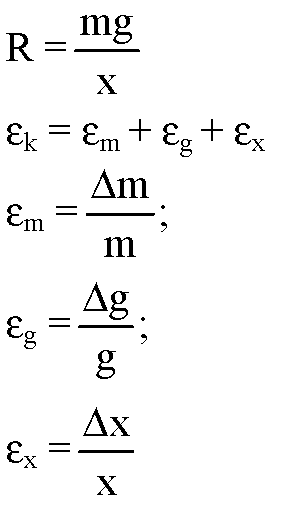
εх максимально когда х — наименьшее, т. е., в нашем случае, для опыта с одним грузом
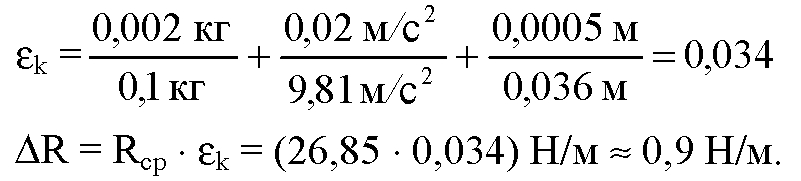
Можно записать результат измерений как:
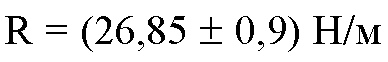
Или округляя:

Т. к. в нашем случае отклонения вычисленных R1; R2; R3; R4 от Rср велики из-за разности условий опытов принимаем