Легко сформулировать множество подобных задач. Но выписанные таблицы не дают ответа на вопрос: каким же правилом руководствоваться для нахождения решения? С целью найти такое правило давайте представим себе задачу иначе — геометрически. Для определенности рассмотрим задачу 56. Обозначим через х и у количество жидкости, содержащейся после какого-либо переливания соответственно в первом и втором бочонках. При переливаниях общее количество жидкости не изменяется, т. е. все время остается равным 4 + 6= 10 ведрам. Поэтому в третьем бо" донке будет находиться 10 — х — у ведер жидкости.
Количество жидкости, содержащейся в бочонке, не может быть больше объема бочонка. Мы видим, что числа х, у удовлетворяют таким условиям:
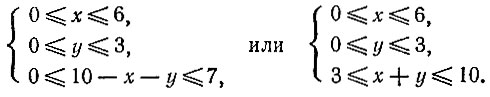
Для дальнейшего удобно воспользоваться листом клетчатой бумаги. Возьмем такой лист, выберем на нем некоторую точку и проведем через нее две перпендикулярные прямые по линиям нанесенной на бумаге решетки. Одну назовем осью X, другую — осью У. Каждой паре чисел х, у мы сможем тогда поставить в соответствие некоторую точку на листе бумаги-точку с координатами х, у. Нарисуем на плоскости все точки, координаты которых удовлетворяют написанным выше неравенствам. На рис. 49 это множество — "внутренняя часть четырехугольника PQRS — заштриховано. Начальному распределению жидкости соответствует на этом рисунке точка А (х = 4, y = 0). Распределению, которое мы хотим получить,- точка В (х = 5, у = 0, при этом в третьем бочонке будет 5 ведер).
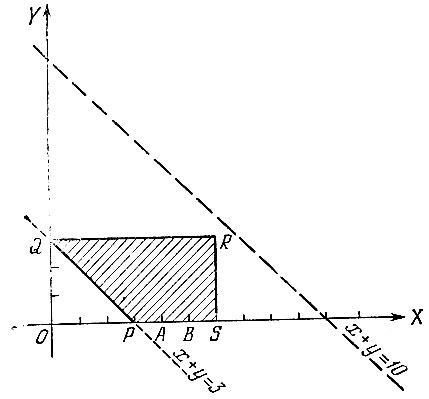
Рис. 49
Последовательность переливаний, ведущая от распределения А к распределению В, представится на этом рисунке в виде некоторой последовательности точек. Или, если мы соединим отрезком прямой линии каждые две последовательные точки,- в виде ломаной с началом в точке А и концом в точке В.
Попробуем выяснить, каким же условиям должны удовлетворять вершины этой ломаной и ее звенья.
Переливание заканчивается, когда наполнится тот бочонок, в который мы льем жидкость, или станет пустым бочонок, из которого мы жидкость выливаем. Это означает, что после каждого переливания обязательно найдется хотя бы один пустой или хотя бы один полный бочонок. Где же на четырехугольнике PQRS будут располагаться соответствующие точки? Если полон первый бочонок (х = 6), то точка лежит на отрезке RS, если первый бочонок пуст (х = 0), то должны быть полными второй и третий бочонки (3 + 7 — 10). Имеется единственная точка с такими условиями — точка Q. Распределениям, при которых пуст второй бочонок (у = 0), соответствуют точки отрезка PS, а если второй бочонок полон (у = 3) — точки отрезка QR. Наконец, третий бочонок пустым быть не может, в первые два бочонка 10 ведер не вместятся, а если он полон, то в первых двух должно содержаться 10 — 7 = 3 ведра (х + у = 3). Соответствующие точки лежат на отрезке PQ. В любом случае точки лежат на границе четырехугольника PQRS. Итак, мы установили, что вершины нашей ломаной должны располагаться на границе четырехугольника PQRS.
Заметим теперь, что при каждом переливании содержимое одного бочонка остается неизменным, ведь каждое переливание затрагивает только два бочонка. Если не изменяется содержимое первого бочонка (х постоянно), то отрезок, соединяющий точки, соответствующие распределениям до и после переливания, параллелен оси У (у начала и конца отрезка координата х имеет одно и то же значение). Если при переливании не меняется содержимое второго бочонка, то соответствующее звено ломаной параллельно оси X (у постоянно). Наконец, если в переливании не участвует третий бочонок, то сохраняется общее количество жидкости в первых двух бочонках. Иными словами, в концах отрезка сумма х+у принимает одно и то же значение. Это означает, что звено ломаной параллельно отрезку PQ. Итак, каждое звено ло* маной перпендикулярно оси ОХ, или оси OY, или биссектрисе угла между этими осями.
Чтобы проверить себя, представим, что некоторое звено ломаной расположено на границе многоугольника PQRS, например на отрезке PQ. Что это означает? Звено образует равные углы с осями X, У, поэтому в переливании не участвует третий бочонок. Кроме того, этот бочонок полон. В первых двух бочонках вместе содержится х + У = 3 ведра жидкости, так что переливание закончится, если станет пустым первый бочонок (х = 0, точка Q) или второй бочонок (у = 0, точка Р). Точно так же можно рассуждать и для других сторон многоугольника PQRS. Мы выяснили, что если некоторое звено ломаной лежит на границе PQRS, то его конец обязательно совпадает с одной из точек Р, Q, R или S.
Наша задача на геометрическом языке выглядит теперь так: соединить точку А с точкой В ломаной, все вершины которой лежат на границе многоугольника, а звенья параллельны осям Х, У или образуют равные углы с осями. При этом, если звено лежит на стороне многоугольника, то его конец должен совпадать с одной из вершин.
В таком виде задача становится нагляднее и требуемые ломаные без труда находятся (рис. 50, 51).
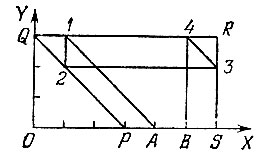
Рис. 50
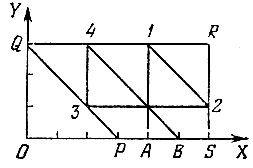
Рис. 51
На клетчатой бумаге проведение ломаных не составляет никакого труда, так как все звенья проходят через узлы решетки, а вершины совпадают с узлами. Ломаные, представленные на рис. 50, 51, соответствуют первому и второму решениям, в чем легко убедиться.
В других задачах роль четырехугольника PQRS могут играть другие многоугольники: параллелограмм (задача 54), пятиугольник (задача 55). Могут вестретиться шестиугольники, причем 6 — это максимальное возможное число сторон. Формулировка задачи при этом остается той же самой, изменятся многоугольник и положения точек А, В.
Геометрическое представление задачи и ее решения наглядно, однако выполнение всех построений отнимает лишнее время, требует бумаги и карандаша. Попробуем на основе геометрических соображений дать рекомендации, как в любой подобной задаче найти требуемый способ (если он существует), не прибегая к построениям.
Вершины многоугольника соответствуют распределениям жидкости, при которых сразу два бочонка находятся в граничном состоянии (оба пусты; оба полны; один пуст, другой полон).
I. Прежде всего нужно добиться с помощью переливаний, чтобы по крайней мере два бочонка находились в граничном состоянии.
Геометрически это соответствует тому, что мы строим ломаную, начинающуюся в точке А и кончающуюся в какой-либо вершине многоугольника.
II. Следует обойти все вершины многоугольника, переливая на каждом шаге жидкость из бочонка, который не участвовал в предыдущем переливании, и не изменяя содержимого одного из бочонков, находя* щихся в граничном состоянии.
Геометрически последовательное применение правила II означает переход от вершины многоугольника к соседней с ним вершине и так далее. Вершин не более шести, поэтому, применив правило II не более шести раз, мы вернемся к распределению, которое нам ранее уже встречалось.
Если, применяя I, мы не попали в Б и если В отлично от вершин многоугольника (применение II не дает нам В), то далее нужно поступать следующим образом.
III. Отправляясь от точки А, а также от распределений, соответствующих каждой вершине многоугольика, совершать переливания, не приводящие к ранее встречавшимся распределениям, пока это будет возможно сделать или встретится распределение Б. При этом, как легко видеть, в переливании должны участвовать бочонок, находящийся в граничном состоянии, и бочонок, не участвовавший в предыдущем переливании.
Из геометрических соображений следует, что если это можно сделать, то единственным способом (из точки А иногда можно провести две ломаные, как в рассмотренной задаче). Если применение правила III не приведет к распределению В, то, значит, переливаниями из A в В перейти невозможно.
