Происхождение задачи о лабиринтах относится к глубокой древности и теряется во мраке легендарных сказаний. Древние,- да, пожалуй, многие и теперь,- задачу о лабиринтах считали вообще неразрешимой. Человек, попавший в лабиринт, не мог уже из него выйти, если только какое-либо чудо или случай не приходили ему на помощь.
Из настоящего раздела мы, наоборот, увидим, что-безвыходных лабиринтов нет, что разобраться и найти выход из самого запутанного лабиринта не составляет особого труда. Решению задачи мы предпошлем историческую справку о лабиринтах.
Слово "лабиринт" — греческое и в переводе означает ходы в подземельях. Существует, действительно, очень много природных подземных пещер с таким огромным количеством по всем направлениям перекрещивающихся коридоров, закоулков и тупиков, что нетрудно в них заблудиться, потеряться и, не найдя выхода, умереть от голода и жажды.
Примеры такого же рода, но уже искусственных лабиринтов, могут представить шахты иных рудников, или так называемые "катакомбы".
Вероятнее всего, что подобные подземелья возбудили у строителей еще древнейших времен желание подражать им искусственными сооружениями. И у древних писателей мы встречаем указание на существование искусственных лабиринтов, например, у египтян. В конце концов, словом "лабиринт" чапхе всего обозначали именно искусственнее чрезвычайно сложное сооружение, составленное из очень большого числа аллей или галерей, бесчисленные разветвления, перекрестки и тупики которых заставляли попавшего туда бесконечно блуждать в тщетных поисках выхода. Об устройстве таких лабиринтов слагались целые легенды.
Известнее всего рассказ о лабиринте, построенном мифическим Дедалом на острове Крит для мифического же царя Миноса. В центре лабиринта жило чудовище Минотавр, и никто из попавших туда не мог выйти обратно, делаясь в конце концов жертвой чудовища. Семь юношей к семь девушек приносили афиняне в дань ежегодно чудовищу, которое прексправно их пожирало. Наконец, Тезей не только убил Минотавра, но и вышел из лабиринта, не заблудившись в нем, при помощи, впрочем, нити из клубка царевны Ариадны. С той поры слова "нить Ариадны" имеют символическое значение как способ, дающий выход из самого затруднительного положения.
Лабиринты бывают самой разнообразной формы и устройства. До наших дней сохранились еще и запутанно-сложные галереи, и ходы пещер, и архитектурные лабиринты над могилами, и извилистые планы на стенах или полах, обозначенные цветным мрамором или черепицей, и извивающиеся тропинки на почве, и рельефные извилины в скалах.
Рисунками лабиринтов украшались одеяния христианских императоров до девятого столетия, и остатки таких же украшений сохранились до сих пор на стенах церквей и соборов того времени. Вероятно, эти украшения служили символом сложности жизненного пути и человеческих заблуждений. Особенно употребительны были лабиринты в первой половине двенадцатого столетия. Во Франции того времени лабиринты выкладывались из камня или изображались на полу церквей и соборов. Они назывались большей частью "путь в Иерусалим" и служили символом трудного земного путешествия в "святые места", наградой за которое является небесная благодать, поэтому центр лабиринта часто называли "небом".
В Англии не встречаются лабиринты на церковном полу, но зато было очень много лабиринтов, сделанных из дерна на лужайках. Они носили различные названия: "Город Троя", "Следы пастуха" и т. п. О таких лабиринтах упоминает Шекспир в своих пьесах "Сон в летнюю ночь" и "Буря".
Все эти лабиринты имеют более исторический, чем математический интерес. Распутать их нетрудно. С течением времени фигуры эти потеряли свое символическое значение и сделались мало-помалу предметом развлечения. Лабиринты переходят в сады, цветники и парки, где путем проведения прихотливо извивающихся, то пересекающихся, то внезапно прегражденных или заканчивающихся тупиком дорожек получались самые запутанные и головоломные фигуры, в которых, действительно, нелегко было найти дорогу от края к центру и где трудно было не заблудиться.
Приведенная историческая справка показывает, насколько стар вопрос о лабиринтах и вместе с тем насколько многих он интересовал в свое время. Люди изощрялись в изобретении самых замысловатых и "безвыходных" лабиринтов. Но, в самом деле, возможно ли построить или даже начертить безвыходный лабиринт, т. е. такой, в котором найти путь к его центру и найти отсюда обратный выход было бы только делом удачи, случая, счастья, а не совершенно определенного и правильного математического расчета?
Разрешение этого вопроса принадлежит сравнительно позднейшему времени, и начало ему положено знаменитым Эйлером. Результаты произведенных в этом отношении изысканий привели к заключению, что нет безвыходных лабиринтов.
Разрешение каждого лабиринта может быть найдено, и притом сравнительно простым путем. Внимательный читатель сам сейчас убедится в этом.
Геометрическая постановка задачи о лабиринтах
Аллеи, дорожки, коридоры, галереи, шахты и т. п. лабиринты тянутся, изгибаясь во все стороны, перекрещиваются, расходятся по всевозможным направлениям, ответвляются, образуют тупики и т. д. Но мы для большей ясности рассмотрения вопроса все перекрестки обозначим просто точками, а все эти аллеи, дорожки, коридоры и т. д. будем принимать просто за линии, прямые или кривые, плоские или нет — все равно, но эти линии соединяют наши точки (перекрестки).
Эти точки и эти линии вместе составляют геометрическую сеть, или лабиринт, если какая-либо точка, движущаяся по линиям этой сети, может прийти к любой другой точке, не покидая линий нашей системы (или сети).
Приняв это, мы докажем, что подобная движущаяся точка (представляющая, например, человека) может последовательно описать все линии сети без всяких скачков и перерывов и при этом по каждой линии сети она пройдет ровно два раза.
Другими словами, лабиринт всегда может быть разрешен.
Но еще раньше, чем приступить к этому доказательству, можно доставить себе довольно интересное математическое развлечение, которое поможет уяснить все предыдущее и весьма полезно будет для усвоения самого доказательства. На листе белой бумаги возьмите произвольно несколько точек и соедините их по две столько раз, сколько хотите, произвольным числом прямых или кривых линий, но так, чтобы ни одна точка системы не осталась совершенно изолированной. Итак, вы получите то, что мы назвали геометрической сетью. Или нарисуйте, например, сеть трамваев или троллейбусов города, сеть железных дорог страны, сеть рек и каналов и т. д., прибавьте к ним, если хотите, границы страны — вы опять получите геометрическую сеть, или лабиринт (для начала, конечно, лучше брать не особенно сложную сеть).
Теперь на куске непросвечивающей бумаги или картона вырежьте небольшое отверстие, через которое была бы видна только небольшая часть составленной вами решетки, или лабиринта. Без такого приспособления в глазах рябит и легко запутаться в сети. Затем направьте окуляр (отверстие для глаза) вашего "экрана" на какой-либо перекресток (точку) вашей сети, например точку, которую назовем Л, и дайте себе такое задание: обежать этим окуляром непрерывно все линии сети два раза (пройти каждый путь вперед и назад) и возвратиться в точку А. Чтобы помнить уже пройденные окуляром линии, примите за правило на каждой проходимой линии ставить поперечную черточку при входе в перекресток и при выходе из него. Отсюда следует, что две оконечности каждого пути от перекрестка до перекрестка (от точки до точки) после выполнения задания (пройти каждую сеть линии два раза) должны быть обозначены двумя поперечными черточками, но не более.
Если мы имеем дело с действительным лабиринтом, или галереями подземных шахт, с разветвлениями пещер и т. д., то блуждающему в этих шахтах вместо черточек на бумаге придется делать уже иной знак, чтобы ориентироваться, и класть, например, камень при входе и выходе из каждого перекрестка — в галерее, которую он покидает, и в той, в которую он входит.
Но обратимся к упомянутому раньше доказательству, что всякий лабиринт разрешим, что нет "безвыходного" лабиринта. Другими словами, решим общую задачу о лабиринтах.
Решение задачи о лабиринтах
Правило I. Отправляемся от начального пункта (первого перекрестка) и идем по какой угодно дороге, пока не приходим или в тупик, или к новому перекрестку. Тогда:
1. Если окажется, что мы попали в тупик, то возвращаемся назад и пройденный путь должен быть 1 уже отброшен, так как мы его прошли два раза (вперед и обратно).
2. Если же мы приходим к новому перекрестку, то направляемся по новому произвольному пути, не забывая только всякий раз отметить поперечной черточкой путь, по которому мы прибыли, и путь, по которому отправились дальше. Как это показано на рис. 188, где мы движемся в направлении, показанном стрелкой f, мы приходим к пересечению путей и берем направление, обозначенное стрелкой g, но тот и другой путь мы обозначаем черточкой (на рисунках крестиками обозначены черточки, поставленные при последнем прохождении через перекресток).
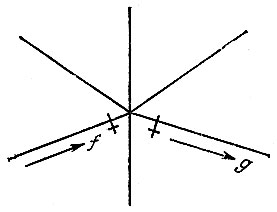
Рис. 188
Мы следуем указанному выше первому правилу всякий раз, когда приходим на такой перекресток, на котором мы еще не были. Но в конце концов мы должны прийти к перекрестку, на котором мы уже были, и здесь может представиться два случая. На известный уже нам пункт мы приходим по дороге, уже раз пройденной нами, или же по пути новому, не отмеченному еще черточкой. Следует придерживаться таких правил:
Правило II. Прибыв на известный уже нам перекресток по новой дороге, мы должны сейчас же повернуть обратно, предварительно отметив этот путь двумя черточками (прибытие и обратное отправление), как это указано на рис. 189.
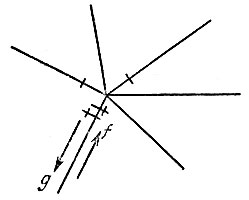
Рис. 189
Правило III. Если мы приходим на известный нам перекресток таким путем, которым уже раз прошли раньше, то, отметив этот путь второй черточкой отправляемся дальше путем, которым мы еще не шли, если только такой путь существует. Этот случай изображен на рис. 190.
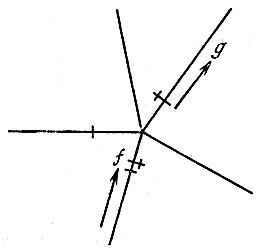
Рис. 190
Но если такого пути нет, то выбираем дорогу, по которой прошли только один раз. Случай этот изображен на рис. 191.
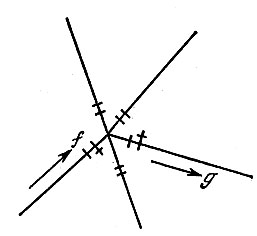
Рис. 191
Придерживаясь точно указанных правил, мы обойдем два раза все линии сети и придем в точку отправления. Это можно доказать, сделав и уяснив себе предварительно такие замечания:
- Выходя из точки отправления, скажем А, мы ставим начальный знак (поперечную черточку).
- Прохождение через перекресток по одному из предыдущих трех правил каждый раз добавляет два знака (две поперечные черточки) на линиях, которые сходятся в этой точке.
- В любой момент прохождения лабиринта, перед прибытием на какой-либо перекресток или после отправления из него, начальный перекресток (пункт отправления) имеет нечетное число знаков (черточек), а всякий другой перекресток имеет их четное число.
- В любой момент, до или после прохода через перекресток, начальный перекресток имеет только один путь, обозначенный только одной черточкой. Всякий же иной из посещенных уже перекрестков может иметь только два пути, обозначенных одной черточкой.
- После полного обхода лабиринта у всех перекрестков все пути должны иметь по две черточки. Это, впрочем, входит прямо в условие задания.
Приняв во внимание все вышеизложенное, мы легко убедимся, что если кто-либо отправляется из начального перекрестка, скажем А, и прибывает в какой-либо иной перекресток М, то он не может встретить таких трудностей задачи, которые могли бы остановить его дальнейшее путешествие. В самом деле, в это место он приходит или новым путем, или путем, который уже один раз пройден. В первом случае прилагается первое или второе из данных выше правил. Во втором случае вступление на перекресток М и остановка здесь дала бы нечетное число знаков около него, следовательно, за неимением нового пути надо пойти по уже пройденному один раз пути, и около перекрестка будет четное число знаков (если он не начальный) по замечанию 3.
Пусть, наконец, мы будем вынуждены закончить наш путь и возвратиться в начальный перекресток А. Назовем эту последнюю линию ZA, т. е. она ведет из перекрестка Z в начальный А. Этот путь должен быть необходимо тем самым, которым мы отправились первый раз из А, иначе путь можно было бы продолжить. И если теперь мы принуждены этим же путем возвратиться в начальную точку, то это значит, что из перекрестка Z нет уже никакого другого пути, который бы не был уже 2 раза пройден. Иначе это значило бы, что забыли применить первую часть правила III, более того, это значило бы, что в Z есть какой-то путь YZ, пройденный только один раз по замечанию 4. Итак, при последнем возвращении в Л все пути в Z должны быть отмечены двумя черточками. Точно так же это можно доказать для предшествующего перекрестка У и для всех остальных. Другими словами, наше предложение доказано, и задача решена.
