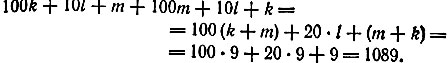Попросите своего товарища написать любое трехзначное число, но только такое, чтобы крайние цифры гличались друг от друга на число, которое вы укаете. Пусть затем он поменяет местами в этом числе крайние цифры. Получится еще одно число. Предложите вашему товарищу вычесть меньшее число из большего. Разность всегда делится на 9, и вы можете всегда сказать наперед, какое будет частное от деления этой разности на 9. Чему же равняется частное?
Решение. Частное равняется указанной вами разности между крайними цифрами числа, умноженной на 11. Например, если взять сначала число 845, то 845 — 548 = 279, 279 : 9 = 33 = (8-5)*11.
Чтобы доказать это правило, заметим, что каждое трехзначное число можно представить в виде 100а + 10b + с, где 0<а ≤ 9 — число сотен, b ≤ 9 — число десятков и с ≤9 — число единиц во взятом числе. Тогда число с переставленными цифрами будет равно 100с + 10b + а. Вычитая второе из первого и деля на 9, имеем
![]()
Эту задачу можно предлагать в следующем более занимательном (особенно для детей) варианте.
Число 1089. Напишите на бумажке число 1089, вложите бумажку в конверт и запечатайте его. Затем предложите кому-нибудь, дав ему этот конверт, написать на нем трехзначное число, но такое, чтобы крайние цифры в нем были различны и отличались бы друг от друга более чем на единицу. Пусть затем он поменяет местами крайние цифры и вычтет из большего трехзначного числа меньшее. В результате пусть он опять переставит крайние цифры и получившееся трехзначное число прибавит к разности первых двух. Когда он получит сумму, предложите ему вскрыть конверт. Там он найдет бумажку с числом 1089, которое, к его удивлению, и есть полученное им число. Почему так произошло?
Решение. Из решения предыдущей задачи мы знаем, что разность между любым трехзначным числом и числом, полученным из него перестановкой крайних цифр, всегда делится на 99. Так как крайние цифры отличаются более чем на единицу, то эта разность обязательно будет трехзначным числом, обозначим ее 100k + 10l + m (0 < k≤9, l≤9, m ≤9). Имеем
![]()
Так как разность делится на 99, то это равенство показывает, что обязательно 10l + m + k = 99, откуда вытекает, что l = 9, m + k = 9. Число с переставленными крайними цифрами имеет вид 100m + 10l + k, и сумма равняется