Изложим теперь способ, который с виду кажется замысловатее других, хотя доказывается очень легко.
Пусть кто-нибудь задумает какое-либо число. Затем предложите ему умножить это число на какое угодно заданное вами другое число, полученное произведение разделить на какое угодно заданное вами число, затем результат опять умножить на какое вам угодно число, это произведение опять разделить на какое угодно заданное вами число и т. д. Если угодно, то можно предоставить тому, кто задумал число, самому умножить и делить задуманное число на какие ему угодно числа, лишь бы он сообщал каждый раз, на какое число он множит и на какое делит. Но, чтобы угадать задуманное число, сам угадывающий пусть в то же время возьмет какое-либо число и проделывает над ним все те же самые умножения и деления, что и задумавший число. Остановившись затем на каком-либо делении, попросите задумавшего число, чтобы он разделил на задуманное им число то последнее число, которое он получил. Точно так же и вы (угадывающий) разделите последнее вами полученное число на взятое вами первоначально. Тогда у вас получится то же число, что и у задумавшего число. После этого пусть задумавший число прибавит к полученному им в уме частному задуманное число и скажет вам результат. Вычитая из этого результата известное уже вам число, получаете задуманное число.
Пример. Пусть кто-нибудь задумает число 5. Предложите ему помножить его на 4; результат (20) разделить на 2 (получится 10), полученное число умножить на 6 (получится 60), это последнее произведение разделить на 4 (получится 15). Но в то же время вы сами должны выбрать какое-либо число и делать над ним все те же действия. Пусть, например, вы возьмете 4 (лучше, вообще, брать для удобства 1). Умножая на 4; вы получаете 16; деля на 2, вы получаете 8; умножая на 6, вы получаете 48; деля это число на 4, вы получаете 12. Вслед за тем вы говорите задумавшему число, чтобы он последнее полученное им число (т.е. 15) разделил на задуманное (т. е. на 5). У него получается 3.
Если вы в то же время свое последнее число 12 разделите на взятое вами сначала, т. е. на 4, то получите также 3. Сделав вид, что вам неизвестно полученное вашим партнером частное, вы говорите ему, чтобы он прибавил к полученному им числу задуманное число и сказал вам результат; он, конечно, скажет вам в этом примере 8. Отнимая от 8 полученное вами уже частное 3, найдете задуманное вашим партнером число 5.
Доказательство. Если над каким-либо числом n производится ряд умножений и делений, то получается результат вида 
Если произвести те же действия над числом р, то получится результат вида 
Оба эти результата, разделенные первый на n, а второй на р, дадут, очевидно, одно и то же число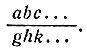 
. Итак, зная число 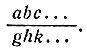сумму 
достаточно из последнего вычесть первое, чтобы получить число n.
Замечание. Можно, очевидно, всячески видоизменять настоящую задачу, так как, во-первых, можно делить и умножать на какие угодно числа, а во-вторых, вместо того, чтобы умножать и делить поочередно, можно сначала умножать два, три и т. д. раза подряд, затем столько же раз делить или наоборот. Можно также, зная последнее частное, заменять сложение вычитанием, если задуманное число, окажется меньше полученного последнего частного, и т. д.