Можно ли из 8 косточек домино сложить квадрат такой, что любая проведённая через него прямая пересекает хотя бы одну косточку? Квадрат, изображенный на рис. 123, не годится, так как прямая АВ не пересекает ни одной косточки.
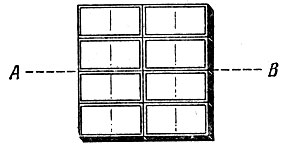
Рис. 123
Решение. Предположим, что такой квадрат сложить можно. Проведем параллельно основанию квадрата три прямые, делящие боковые стороны квадрата на четыре равные части. По условию каждая из проведенных прямых пересечет хотя бы одну косточку домино. Но над любой из прямых лежит четное число (4, 8 или 12) маленьких квадратов, равных половине косточки. Поэтому каждая прямая пересекает четное число косточек и, значит, не меньше двух. Таким образом, проведенные прямые пересекают не менее шести косточек. Если теперь аналогичным образом провести три прямые, параллельные боковым сторонам, то и они должны пересечь не менее шести косточек. Поскольку ни одна косточка не может пересекаться двумя прямыми, то в нашем квадрате должны присутствовать по крайней мере 12 косточек, что невозможно.
