Мы встречались уже в этом разделе с вопросом, может ли конь обойти часть шахматной доски, побывав при этом на каждом поле только один раз.
Вот еще одна старинная задача о ходе шахматного коня:
Требуется обойти конем все 64 клетки шахматной доски так, чтобы на каждой клетке конь был только один раз и затем возвратился бы в клетку, из которой вышел.
Задачей этой занимался Эйлер и в письме к Гольдбаху (26 апреля 1757 года) дал одно из решений ее. Вот что, между прочим, пишет он в этом интересном письме:
"… Воспоминание о предложенной когда-то мне задаче послужило для меня недавно поводом к некоторым тонким изысканиям, в которых обыкновенный анализ, как кажется, не имеет никакого применения. Вопрос состоит в следующем. Требуется обойти шахматным конем все 64 клетки шахматной доски так, чтобы на каждой клетке он побывал только один раз. С этой целью все места, которые занимал конь при своих последовательных ходах, закрывались марками. Но к этому присоединилось еще требование, чтобы начало хода делалось с данного места. Это последнее условие казалось мне очень затрудняющим вопрос, так как я скоро нашел некоторые пути, при которых, однако, выбор начала для меня свободен. Я утверждаю, однако, что если полный обход коня будет возвратный, т. е. если конь из последнего места опять может перейти на первое, то устраняется и это затруднение. После некоторых изысканий по этому поводу я нашел, наконец, ясный способ находить сколько угодно подобных решений (число их, однако, не бесконечно), не делая проб. Подобное решение представлено на рисунке (рис. 153).
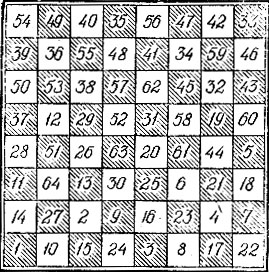
Рис. 153
Конь ходит в порядке, указанном числами. Так как из последнего места 64 он может перейти на 1, то этот полный ход есть возвратный".
Таково решение задачи о ходе шахматного коня, данное Эйлером. В письме не указаны ни приемы, ни путь, которыми знаменитый ученый пришел к своему открытию. Сейчас мы укажем на методы иных, более симметричных и методичных решений.
I
Разделим шахматную доску на две части: внутреннюю, состоящую из 16 клеток, и краевую (рис. 154).

Рис. 154
Каждые 12 клеток краевой доски, обозначенные у нас Одинаковыми буквами, дают один из частных зигзагообразных путей шахматного коня вокруг доски; точно так же четыре одноименные клетки внутренней части доски дают частный замкнутый путь шахматного коня в виде квадрата или в виде ромба. Рис. 155 представляет два зигзагообразных частных пути коня на краевой части доски. Эти пути обозначим буквами а и b. Там же начерчены и два пути на внутренней части доски. Эти пути назовем a’ и b’ соответственно обозначениям на рис. 154.
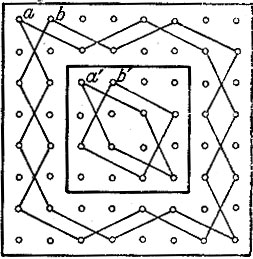
Рис. 155
Закончив какой-нибудь частный круговой путь по краевой части доски, конь может перескочить на любой из трех путей другого наименования на внутренней части доски. Нетрудно (стоит лишь взять в руки шахматную доску и коня) найти, и притом различными способами, четыре пути из 16 клеток — таких, например, как
ab’, bc’, cd’, da’.
В самом деле, всмотритесь в рис. 154 и 155 или поставьте перед собой шахматную доску, и вы увидите, что для получения частного пути коня в 16 клеток надо только краевой частный круговой путь из 12 клеток соединить с внутренним путем, но другого наименования, прямой чертой, уничтожая при этом в каждом из частных круговых путей замыкающую линию. Так получим четыре частных круговых пути по 16 клеток. Эти четыре частных . пути по 16 клеток опять можно соединить различным образом и получить полный путь шахматного коня из 64 клеток.
Итак, ставят коня на какую-нибудь клетку, например, краевой части доски и описывают по ней путь из 12 клеток; вслед за тем конь перепрыгивает на клетку одного из трех (не одноименных) внутренних путей, проходит этот путь в любом направлении и перескакивает опять на краевую часть, где снова делает следующий частный зигзагообразный путь из 12 клеток, вновь перескакивает на один из внутренних, не одноименных с предыдущим, путей, описывает его, переходит опять на новый краевой путь и т. д., пока не обойдет все 64 клетки.
Способ решения задачи настолько прост и легок, что не нуждается в более подробных разъяснениях и указаниях.
II
Можно эту же задачу решить и другим, не менее легким, приемом. Здесь для удобства доска делится на 4 части по 16 клеток в каждой двумя серединными линиями (рис. 156) 16 клеток каждой четверти, обозначенных одинаковыми буквами, можно соединить посредством сторон двух квадратов и двух ромбов, не имеющих ни одной общей вершины (рис. 157). Соединяя, в свою очередь, одноименные квадраты и ромбы всех четвертей доски, можно получить четыре частных круговых возвратных пути из 16 клеток. Соединяя затем эти последние пути, получим полный путь коня в 64 клетки.

Рис. 156
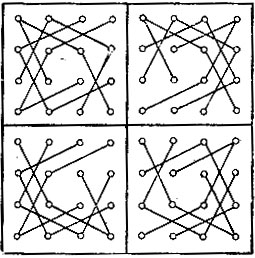
Рис. 157
Полезно сделать еще следующие замечания. На каждой четверти доски ромбами и квадратами обозначены по четыре пути коня. Если соединим ромбы и квадраты, обозначенные одинаковыми буквами во всех четырех четвертях доски, получим по четыре частных возвратных пути из 16 клеток.
Некоторые трудности могут представиться кому-нибудь, когда для получения полного пути в 64 клетки он начинает соединять между собой эти четыре частных пути по 16 клеток. Здесь полезно иметь в виду, что цепь (или ряд ходов) можно видоизменять, не разрывая ее. Основано это на так называемом правиле Бертрана, которое состоит в следующем.
Пусть имеем незамкнутую цепь ходов, проходящих через клетки A, B, С, D, E, F, G, H, I, J, К, L и пусть оконечности этой цепи будут А и L. Если клетка, например D, отличная от предпоследней K, находится от последней L на расстоянии хода коня, то DE можно заменить через DL и цепь ходов обратится в
ABCDLKJIHGFE,
т. е. вторая половина цепи будет пройдена в обратном порядке.
То же самое относится и к тому случаю, когда какая-нибудь клетка, кроме второй, сообщается ходом коня с первой. Итак, цепь (или ряд ходов) можно видоизменять, не разрывая ее.
Число путей, которыми конь может обойти доску и которые можно найти указанными выше приемами, не бесконечно. Но оно настолько огромно, что трудно его представить.
