В квадрате, состоящем из 16 клеток, расставить четыре буквы так, чтобы в каждом горизонтальном ряду, в каждом вертикальном ряду и в каждой диагонали встречалась только одна буква. Как велико число решений этой задачи при одинаковых и разных буквах?
Решение. Прежде всего предположим, что буквы одинаковы. Поставим одну букву в какой-нибудь клетке первой диагонали. При этом на второй диагонали окажутся запрещенными две клетки, стоящие в одном горизонтальном и вертикальном ряду с уже занятой клеткой. В одной из остальных двух клеток второй диагонали можно поставить вторую букву. Далее легко заметить, что две буквы, поставленные на диагоналях, однозначно определяют расстановку в соответствии с условиями задачи двух оставшихся букв (рис. 166). Итак, если фиксировать место буквы на первой диагонали, то задача имеет два решения. Но так как первую букву можно поставить в любой клетке первой диагонали, то задача имеет 2*4 = 8 решений. Так как четыре различных буквы можно перемещать 24 способами, то в этом случае задача имеет 8*24 = 192 решения"
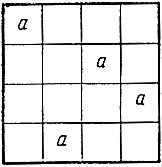
Рис. 166
