В квадрате, состоящем из 16 клеток, расставить 16 букв (четыре буквы а, четыре b, четыре с, четыре d) так, чтобы в каждом горизонтальном ряду и в каждом вертикальном ряду любая буква встречалась только один раз.
Решение. Предположим, что мы расставим буквы так, как это требуется в задаче. Поменяем местами какие-либо два столбца или две строки При этом получится новое расположение букв, также удовлетворяющее условию задачи. Очевидно столбцы и строки можно переставить так что в верхней строке и крайнем левом столбце буквы разместятся в таком порядке, как показано на рис. 167. Подобные расположения букв будем называть основными. Найдем теперь все основные расстановки букв. Легко видеть, что во второй строке буквы а, с, d можно разместить только тремя способами: (c, d, a), (d, a, c(, (a, d, c). Первым двум соответствуют единственные расположения букв в третьей и четвертой строках, третьему соответствуют два расположения. Итак, имеется всего четыре основных размещения букв, представленных на рис. 168.
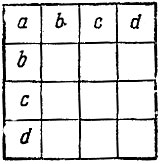
Рис. 167
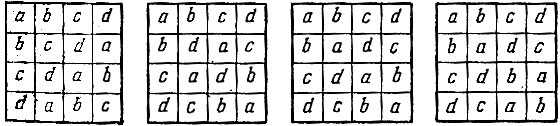
Рис. 168
Из каждого основного перестановкой столбцов можно получить 24 новых размещения. А при каждом расположении столбцов перестановкой второй, третьей и четвертой строк — еще 6 новых. Очевидно, все эти Расположения различны. Итак, существует 4*24*6 = 576 различных расстановок букв, удовлетворяющих условию задачи.
Аналогичный вопрос можно поставить для квадрата, состоящего из 25, 36 и в общем случае n2 клеток. Квадратная таблица, в которой каждый ряд является перестановкой некоторого числа различных букв или цифр, причем в каждом столбце буквы или цифры различны, называется латинским квадратом. Такие квадраты впервые изучал Эйлер в 1782 году. Термин "латинские" связан с тем, что элементы квадрата обозначались латинскими буквами а, b, с,… Количество различных латинских квадратов из n2 клеток очень быстро растет с увеличением числа n. Условимся обозначать через k! произведение всех целых чисел от 1 до k, k! = 1*2*3 … k. Известно, что существует не менее чем n!*(n — 1)! … 2!*1! латинских квадратов размером n*n. Точное значение этого количества известно только при маленьких n.
