Попробуем теперь решить другую задачу, Б которой имеем два острова, соединенных между собой и с берегами реки 15 мостами, как это указано на прилагаемом рисунке (рис. 179).
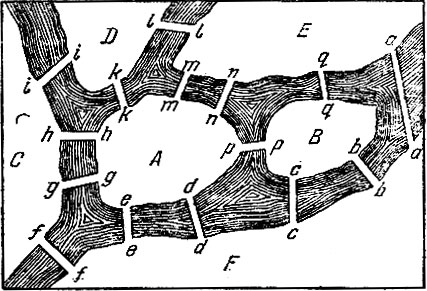
Рис. 179
Спрашивается, можно ли за один раз обойти все эти мосты, не проходя ни через один более одного раза?
Решение. Согласно выведенным нами уже раньше приемам решения, обозначаем разными буквами все местности, разделенные различными рукавами реки и соединенные мостами. После этого составляем следующую таблицу:

Отсюда делаем вывод, что задача разрешима, ибо число повторений букв на единицу больше числа мостов. Кроме того, по предыдущему знаем, что обход должен начаться из нечетной местности D или Е. Искомый обход мостов может быть сделан так:
EaFbBcFdAeFfCgAhCiDkAmEnApBqElD,
или в обратном порядке. Маленькие буквы среди больших показывают, какие именно переходятся мосты.
Изложенные выше приемы решения задачи прежде всего позволяют судить об ее разрешимости или неразрешимости. Сделаем теперь еще несколько выводов, ведущих к более определенному уяснению подобных задач.
Заметим прежде всего, что сумма чисел второго столбца точно равна двойному количеству мостов. Это зависит от того, что в каждом мосту мы считаем оба его конца, упирающиеся в различные берега. Отсюда нетрудно вывести следующее:
1) Сумма чисел второго столбца всегда должна быть четной, ибо половина ее должна дать число мостов.
2) Значит, если задача разрешима, то в ней или нет совсем нечетных местностей, или же они есть в четном количестве (однако не более двух, как увидим сейчас ниже). Иначе второй столбец при сложении не давал бы четного числа.
3) Если в задаче все местности четные, то задача всегда разрешима, из какой бы местности мы ни отправлялись.
Так, например, задачу 167 можно было бы решить, если бы задано было обойти все мосты по два раза каждый, что сводится, в сущности, к удвоению числа мостов, т. е. к обращению всех данных местностей в четные.
4) Если в задаче есть только две нечетные местности, а остальные все четные, то сумма цифр третьего столбца на единицу больше числа мостов, и задача разрешима, если начать обход мостов с одной из двух нечетных местностей. Но если число нечетных местностей будет более двух, т.е. 4, 6, 8 и т. д., то задача оказывается неразрешимой, так как сумма чисел третьего столбца будет более числа мостов на 2, на 3, на 4 и т. д. единицы.
Вообще, при всяком данном расположении мостов сразу нетрудно определить случай разрешимости или неразрешимости задачи. Задача неразрешима, если число нечетных местностей более двух. Задача разрешима, если 1) все местности четные и 2) если нечетных местностей только две. В последнем случае обход мостов надо начинать с одной из этих нечетных местностей.
Докажем, что если все местности четные, то существует замкнутый путь (кончающийся в местности, с которой он начался), проходящий по каждому мосту ровно один раз. Будем называть длиной пути количество мостов, по которым этот путь проходит. Так, длина пути из решения задачи 168 равна 15. Среди всех путей, которые можно провести по нашим местностям с соблюдением условия задачи, выберем самый длинный путь и обозначим его abc … g (где буквы а, b, с, …, g — это названия мостов, пересекаемых путем). Обозначим через А местность, в которой он начинается, и предположим, что он заканчивается в местности G, отличной от А. Если путь ранее проходил через G, скажем, r раз, то, двигаясь по нему, мы должны были уже пройти 2r мостов, ведущих в G. Поскольку местность G четная, то, войдя в нее по мосту g, мы должны найти еще один мост h, ведущий из G и отличный от уже пройденных 2r мостов и моста g. Это означает, что мы можем продолжить путешествие и далее, в противоречие с тем, что выбранный путь имеет максимальную длину. Итак, путь abc … g кончается в местности А, с которой начался, т. е. он замкнут. Покажем теперь, что он проходит через каждый мост. Предположим, что он не проходит через некоторый мост f. Ясно, что мост f можно выбрать так, что через одну из соединяемых им местностей проходит путь abc … g. Для определенности предположим, что f ведет в местность В, из которой выходят мосты а, b. Тогда путь fbc … g, a имеет длину, на единицу большую, чем abc … g. Но мы обозначили через abc … g самый длинный путь, который только можно провести по нашим местностям. Полученное противоречие доказывает, что путь abc … g проходит через все мосты.
Докажем теперь, что требуемый путь существует и во втором случае, когда есть только две нечетные местности, скажем, А и В. Построим новый мост а, соединяющий А и В. Тогда все местности станут четными и, по доказанному выше, существует путь, про* ходящий по одному разу через все мосты. Этот путь замкнут, следовательно, его можно начинать с любого моста, например с моста a: abc … g. Легко видеть, что путь bc … g, концы которого лежат в местностях А и В, решает нашу задачу.
Исследовав задачу и сделав вывод о ее разрешимости, остается только совершить самый обход мостов. Но это уже сравнительно легкая часть задачи.
