Трое крестьян, Иван, Петр и Алексей, пришли на рынок с женами: Марией, Екатериной и Анной. Кто на ком женат, нам не известно. Требуется узнать это на основании следующих данных: каждый из этих шести человек заплатил за каждый купленный предмет столько копеек, сколько предметов он купил. Каждый мужчина истратил на 48 копеек больше своей жены. Кроме того, Иван купил на 9 предметов больше Екатерины, а Петр — на 7 предметов больше Марии. Решение. Если один из мужчин купил, скажем, х предметов, то по условию он заплатил за них х2 копеек. Если его жена купила у предметов, то она заплатила за них у2 копеек. Значит, имеем х2 — у2 = 48, или (х — у)*(х + у) = 48.
Числа х, у по условию целые и положительные. Это возможно только в том случае, когда х — у и х + у четны и х + у > х — у. Разлагая 48 на сомножители, видим, что имеется только три удовлетворяющие этому условию возможности: 48 = 2*24 = 4*12 = 6*8, или
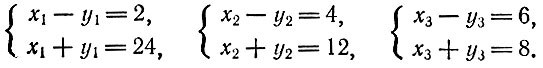
Решая эти системы уравнений, находим x1 = 13, у1 = 11, х2 = 8, у2 = 4, х3 = 7, у3 = 1.
Отыскивая те значения х и у, разность которых равна 9, находим, что Иван купил 13 предметов, Екатерина — 4 предмета. Точно так же Петр купил 8 предметов, Мария — 1 предмет. Таким образом, имеем следующие пары:

