Общеизвестная коробочка с 15 нумерованными квадратными шашками имеет любопытную историю, о которой мало кто из игроков подозревает. Расскажем о ней словами немецкого исследователя игр, математика В. Аренса.
Около полувека назад — в конце 70-х годов — вынырнула в Соединенных Штатах игра в 15; она быстро распространилась и, благодаря несчетному числу игроков, которых она заполонила, превратилась в настоящее общественное бедствие.
То же наблюдалось по эту сторону океана, в Европе. Здесь можно было даже в конках видеть в руках пассажиров коробочки с 15 шашками. В конторах и магазинах хозяева приходили в отчаяние от увлечения своих служащих и вынуждены были воспретить им игру в часы занятий и торговли. Содержатели увеселительных заведений ловко использовали эту манию и устраивали большие игорные турниры.
Игра проникла даже в торжественные залы германского рейхстага. Как сейчас вижу в рейхстаге седовласых людей, сосредоточенно рассматривающих в своих руках квадратную коробочку, — вспоминает известный географ и математик Зигмунд Гюнтер, бывший депутатом в годы игорной эпидемии.
Рис. 9. Игра в 15
В Париже игра эта нашла себе приют под открытым небом, на бульварах, и быстро распространилась из столицы по всей провинции. Не было такого уединенного сельского домика, где не гнездился бы этот паук, подстерегая жертву, готовую запутаться в его сетях, — писал один французский автор.
В 1880 г. игорная лихорадка достигла, по-видимому, своей высшей точки. Но вскоре после этого тиран был повержен и побежден оружием математики. Математическая теория игры обнаружила, что из многочисленных задач, которые могут быть предложены, разрешима только половина; другая не разрешима никакими ухищрениями.
Стало ясно, почему иные задачи не поддавались самым упорным усилиям, и почему устроители турниров отваживались назначать огромные премии за разрешения задач. В этом отношении всех превзошел изобретатель игры, предложивший издателю нью-йоркской газеты для воскресного приложения неразрешимую задачу с премией в 1000 долларов за ее разрешение; так как издатель колебался, то изобретатель выразил полную готовность внести названную сумму из собственного кармана. Имя изобретателя Самуэль (Сэм) Лойд. Он приобрел широкую известность как составитель остроумных задач и множества головоломок. Любопытно, что получить в Америке патент на придуманную игру ему не удалось. Согласно инструкции, он должен был представить рабочую модель для исполнения пробной партии; он предложил чиновнику патентного бюро задачу, и когда последний осведомился, разрешима ли она, изобретатель должен был ответить: Нет, это математически невозможно. В таком случае, — последовало возражение, — не может быть и рабочей модели, а без модели нет и патента. Лойд удовлетворился этой резолюцией, — но, вероятно, был бы более настойчив, если бы предвидел неслыханный успех своего изобретения*.
* (Этот эпизод использован Марком Твэном в его романе Американский претендент.)
Приведем собственный рассказ изобретателя игры о некоторых фактах из ее истории:
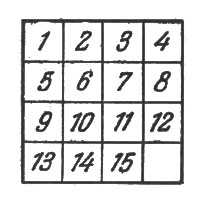
Рис. 10. Игра в 15
Давнишние обитатели царства смекалки, — пишет Лойд, — помнят, как в начале 70-х годов я заставил весь мир ломать голову над коробкой с подвижными шашками, получившей известность под именем игры в 15 (рис. 10). Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14 и 15 были переставлены, как показано на прилагаемой иллюстрации (рис. 11). Задача состояла в том, чтобы, последовательно передвигая шашки, привести их в нормальное положение, причем, однако, порядок шашек 14 и 15 должен быть исправлен.
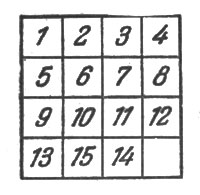
Рис. 11. Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14 и 15 были переставлены
Премия в 1000 долларов, предложенная за первое правильное решение этой задачи, никем не была заслужена, хотя все без устали решали эту задачу. Рассказывали забавные истории о торговцах, забывавших из-за этого открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Никто не желал отказаться от поисков решения, так как все чувствовали уверенность в ожидающем их успехе. Штурманы, говорят, из-за игры сажали на мель свои суда, машинисты проводили поезда мимо станций; фермеры забрасывали свои плуги.
* * *
Познакомим читателя с начатками теории этой игры. В полном виде она очень сложна и тесно примыкает к одному из отделов высшей алгебры (теория определителей). Мы ограничимся лишь некоторыми соображениями, изложенными В. Аренсом.
Задача игры состоит обыкновенно в том, чтобы посредством последовательных передвижений, допускаемых наличием свободного поля, перевести любое начальное расположение 15 шашек в нормальное, т. е. в такое, при котором шашки идут в порядке своих чисел: в верхнем левом углу 1, направо — 2, затем 3, потом в верхнем правом углу 4; в следующем ряду слева направо: 5, 6, 7, 8 и т. д. Такое нормальное конечное расположение мы даем здесь на рис. 10.
Вообразите теперь расположение, при котором 15 шашек размещены в пестром беспорядке. Рядом передвижений всегда можно привести шашку 1 на место, занимаемое ею на рисунке.
Точно так же возможно, не трогая шашки 1, привести шашку 2 на соседнее место вправо. Затем, не трогая шашек 1 и 2, можно поместить шашки 3 и 4 на их нормальные места: если они случайно не находятся в двух последних вертикальных рядах, то легко привести их в эту область и затем рядом передвижений достичь желаемого результата. Теперь верхняя строка 1, 2, 3, 4 приведена в порядок, и при дальнейших манипуляциях с шашками мы трогать этого ряда не будем. Таким же путем стараемся мы привести в порядок и вторую строку: 5, 6, 7, 8; легко убедиться, что это всегда достижимо. Далее, на пространстве двух последних рядов необходимо привести в нормальное положение шашки 9 и 13; это тоже всегда возможно. Из всех приведенных в порядок шашек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 13 в дальнейшем ни одной не перемещают; остается небольшой участок в шесть полей, в котором одно свободно, а пять остальных заняты шашками 10, 11, 12, 14, 15 в произвольном порядке. В пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12. Когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке, либо в обратном (рис. 11). Таким путем, который читатели легко могут проверить на деле, мы приходим к следующему результату.
Любое начальное положение может быть приведено к расположению либо рис. 10 (положение I), либо рис. 11 (положение II).
Если некоторое расположение, которое для краткости обозначим буквою S, может быть преобразовано в положение I, то, очевидно, возможно и обратное — перевести положение I в положение S. Ведь все ходы шашек обратимы: если, например, в схеме I мы можем шашку 12 поместить на свободное поле, то можно ход этот тотчас взять обратно противоположными движениями.
Итак, мы имеем две такие серии расположений, что положения одной серии могут быть переведены в нормальное I, а другой серии — в положение II. И наоборот, из нормального расположения можно получить любое положение первой серии, а из расположения II — любое положение второй серии. Наконец, два любых расположения, принадлежащих к одной и той же серии, могут быть переводимы друг в друга.
Нельзя ли идти дальше и объединить эти два расположения — I и II? Можно строго доказать (не станем входить в подробности), что положения эти не превращаются одно в другое никаким числом ходов. Поэтому все огромное число размещений шашек распадается на две разобщенные серии:
- На те, которые могут быть переведены в нормальное I: это — положения разрешимые,
- На те, которые могут быть переведены в положение II и, следовательно, ни при каких обстоятельствах не переводятся в нормальное расположение: это — положения, за разрешение которых назначались огромные премии.

Рис. 12. ‘…о почтенных чиновниках, целые ночи напролет простаивавших под фонарем…’
Как узнать, принадлежит ли заданное расположение к первой или ко второй серии? Пример разъяснит это.
Рассмотрим такое расположение.
Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в нормальном расположении принадлежит 8. Шашка 9 стоит, значит, ранее шашки 8: такое упреждение нормального порядка называют беспорядком. О шашке 9 мы скажем: здесь имеет место 1 беспорядок. Рассматривая дальнейшие шашки, обнаруживаем упреждение для шашки 14; она поставлена на три места (шашек 12, 13. 11) ранее своего нормального положения; здесь у нас 3 беспорядка (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1+3=4 беспорядка. Далее, шашка 12 помещена ранее шашки 11, и точно так же шашка 13 ранее шашки 11. Это дает еще 2 беспорядка. Итого имеем 6 беспорядков. Подобным образом для каждого расположения устанавливают общее число беспорядков, освободив предварительно последнее место в правом нижнем углу. Если общее число беспорядков, как в рассмотренном случае, четное, то заданное расположение может быть приведено к нормальному конечному; другими словами, оно принадлежит к разрешимым. Если же число беспорядков нечетное, то расположение принадлежит ко второй серии, т. е. к неразрешимым (нуль беспорядков принимается за четное число их).
Благодаря ясности, внесенной в эту игру математикой, прежняя лихорадочная страстность в увлечении сейчас совершенно немыслима. Математика создала исчерпывающую теорию игры, теорию, не оставляющую ни одного сомнительного пункта. Исход игры зависит не от каких-либо случайностей, не от находчивости, как в других играх, а от чисто математических факторов, предопределяющих его с безусловной достоверностью. Обратимся теперь к головоломкам в этой области. Вот несколько разрешимых задач, придуманных изобретателем игры:
