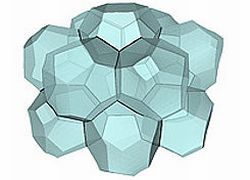
Учеными из института Бата был построен очередной контрпример к задаче Кельвина. Даже не смотря на то, что этот новый контрпример не самый мальнький из известных, математики создали удобную технологию по генерированию контрпримеров, благодаря которой можно получать их в гораздо большом количестве. Статья ученых была напечатана в журнале под названием Philosophical Magazine Letters, а короткое изложение этой статьи приведен в пресс-релизе на интернет-сайте университета.
Задачу Келльвина относят к класическим нерешенным задачам по математике. Ее формулировка свучит так: нужно предъявить такой график распределения многогранников одного объема в пространстве, чтобы пространство стенок разбиения была максимально малой. Данная задача возникает, к примеру, во время описания строения пены. В свою очередь, гипотеза Кельвина заключается в том, что решением задачи будет разбиения пространства на равно узрезанные октаэдры.
В данный момент известно ряд контрпримеров к этой гипотезе.. А именно, в 1993 году Филан и Уири предложили разбиение с более маленькой площадью, чем у разбиения Кельвина. Вошли в него два сорта фигур – многогранники с двенадцатью и четырнадцатью гранями.
В новом контрпримере вмещает в себя многогранники четырех разных типов. Основной особенностью такой вот схемы является тот факт, что ее получили уже после того как был проведен анализ трехмерного примера Свифта-Хоенберга. Сами ученые говорят, что дальнейшее развитие этого способа даст возможность получить контрпримеры к гораздо большем количестве, может быть, даже с меньшей площадью, чем в данный момент известные.
Не так давно ученые из Принстона поставили новый рекорд по плотной запоковке тетраэдров в трехмерном замкнутом объеме. При использовании компьютерного моделирования, ученым удалось добиться того, что плотность упаковки равнялась 0,782. Рекорд, который был поставлен перед этим составил 0,778, и установили его в 2006 году в том же университете.
