Дано:
Доска массой M1 может двигаться без трения по наклонной плоскости с углом наклона alfa к горизонту. В каком направлении и с каким ускорением должна бежать по доске собака с массой M2, чтобы доска не соскальзывала с наклонной плоскости?
Решение №1 (неправильное)
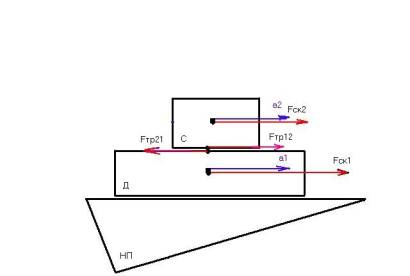
Чтобы доска (тело1) не соскальзывала (=не двигалась вниз) по наклонной плоскости (под действием силы скатывания Fск1= m1*g*sin(alfa)), сила трения со стороны собаки (Fтр21= Fтр) должна быть направлена вверх. Поэтому собака должна бежать вниз. При этом на собаку (тело2) действует сила скатывания Fск2= m2*g*sin(alfa) и сила трения Fтр12, направленная противоположно (то есть вниз: Fтр12= -Fтр) (рис.1).
Рис.1
Получаются следующие уравнения движения:
M1*a1= Fск1-Fтр= 0
M2*a2= Fск2+Fтр
Отсюда Fтр= Fск1 => a2= (Fск2+ Fск1)/M2.
Это решение приведено в [пособие для поступающих в вузы: В.А.Колесников. Физика. Теория и методы решения конкурсных задач. Часть 1, с.40]. Но это решение ущербно потому, что оно использует некорректный закон трения (подробнее критику этого закона трения (и корректный закон трения) смотри в Паралогизмы в физике) и поэтому дает существенно неверный (не имеющий физического (а точнее – практического, потому что формально он верен) смысла) результат: собака разгоняется по доске до «бешенной» скорости (a1= const не=0), а доска продолжает скользить вниз (хотя и с постоянной скоростью: a1=0). То есть относительная скорость между ними возрастает до бесконечности.
В решении есть и еще одна ошибка (больше похожая на софизм). Если (при движении доски вниз) собака движется вниз, то сила трения, действующая на неё, (согласно закону трения) направлена противоположно, то есть вверх! А не вниз, как сказано в решении. И никого этого не смущает. Почему не смущает? Потому что имеется в виду всё-таки, что собака, как и сказано в условии задачи, бежит, а не скользит (по наклонной плоскости) В этом случае, действительно, при движении (беге) вниз она (за счет трения) будет отталкивать от себя доску в противоположном направлении – вверх. Но ведь это – совершенно другая механическая картина! Это совершенно другой тип движения! Поскольку бег или ходьба аналогичны вращению ног собаки относительно осей бедренных суставов (для простоты положим, что коленные суставы отсутствуют).
Таким образом, здесь произведена подмена понятий: движение (то есть скольжение) на бег (=вращение ног) (поскольку при движении собаки вниз сила трения, от неё на доску, положена направленной вверх), а потом обратно (поскольку в решение не введены (после этого) параметры вращения).
Решение №2 (промежуточное)
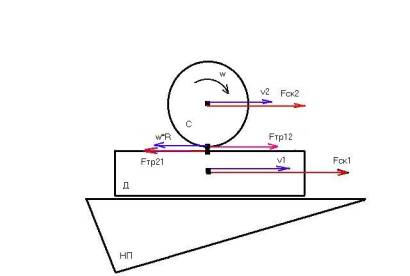
Итак, правильное решение предполагает введение в модель (задачной ситуации) еще и вращения. Пусть длина ноги (собаки)– R, её момент инерции – J2, угловое ускорение – e. На ногу собаки будет действовать момент силы трения Fтр*R (рис.2).
В решении добавится уравнение (3) – для вращения. В итоге:
M1*a1= Fск1-Fтр= 0
M2*a2= Fск2+Fтр
J2*e= -Fтр*R (3),
где a2 – ускорение оси бедренного сустава собаки (для простоты считаем, что она проходит через центр масс собаки).
При этом, согласно закону трения, Fтр= r*f(v1-(v2-w*R)) – некая (нечетная) функция от скорости доски относительно подошвы ноги собаки (v2-w*R). Поэтому все уравнения системы – дифференциальные (ведь в левых их частях стоят ускорения – производные скоростей, входящих в выражение для Fтр).
Анализ решения этой системы показывает, что не найдется ни одной комбинации исходных условий задачи (M1, M2, J2, r, R, w20
(Это — начальная угловая скорость ног собаки, остальные скорости (v1, v2) в исходном состоянии считаем =0.
Кстати: в условии задачи даны только 2 параметра из этого списка. Поэтому, строго говоря, задача не (в такой формулировке) является неразрешимой.)),
при которых получалось бы то, что требуется в условии задачи (отсутствие соскальзывания доски): v1= const(t)=0 (или хотя бы limit(v1(t), t=infinity)= const(t)= 0).
Решение №3 (правильное)
Но не упустили ли мы что-нибудь из виду? В исходных условиях? Ведь собака же не просто (пассивно) стоит ногами на доске (как получается в вышеприведенной модели), она еще прилагает к ним (ногам) свою мускульную силу (чтобы именно бежать). Эту мускульную силу и отобразит момент вращения Mw2, который мы добавим в (3). Получаем в итоге следующую систему дифференциальных уравнений:
M1*a1= Fск1-Fтр= 0
M2*a2= Fск2+Fтр
J2*e= -Fтр*R +Mw2 (3)
Анализ решения этой системы обнаруживает, что искомое решение v1= const(t)=0 получается при следующих условиях, налагаемых на исходные параметры задачи:
M= M2/M1
F1= M1*g*sin(alfa);
A= M1*w20^2*R/F1;
D= Mw2/F1/R;
B= r*w20*R/F1 =1;
C= J2*w20^2/(F1*R)= -M*A*(-D+1)/(M+1)
В частном случае, соответствующем предыдущему решению (D=0), получаем условие C<0, что не имеет физического смысла (см. определение параметра C).
Комментарий для преподавателей
Если бы создатели задачи хотели её простого (и корректного) решения, то им бы следовало заменить в условии собаку на кирпич, а бег – на волочение (кирпича) по доске.
Тогда, чтобы доска не соскальзывала (v1=0), кирпич должен двигаться (по доске) вверх. И причем с такой скоростью, чтобы сила трения между доской и собакой уравновесила силу скатывания: Fск1= Fтр. То есть именно скорость кирпича (а не ускорение) является условием отсутствия скатывания. Причем за счет чего она будет создаваться – совершенно не важно Определить эту скорость можно только, если известен закон трения (который в условии не дан). В простейшем же случае (зона покоя) скорость кирпича должна равняться 0. Но при этом – не равна 0 сила тяги, действующая на него.